搜索
【题目】如图，已知等腰△ABC的底边BC＝13cm，D是腰AB上一点，且CD＝12cm， BD＝5cm．
（1）求证：△BDC是直角三角形；
（2）求△ABC的周长
参考答案：
【答案】（1）证明见解析；（2）△ABC的周长为
．
【解析】
（1）由BC=13cm，CD=12cm，BD=5cm，知道BC2=BD2+CD2，所以△BDC为直角三角形，
（2）由（1）可求出AC的长，周长即可求出．
（1）证明：∵BC＝13cm，CD＝12cm，BD＝5cm，
∴BC2＝BD2+CD2
∴△BDC为直角三角形；
（2）解：设AB＝x，
∵△ABC是等腰三角形，
∴AB＝AC＝x，
∵AC2＝AD2+CD2
x2＝（x﹣5）2+122，
解得：x＝
，
∴△ABC的周长＝2AB+BC＝2×+13＝．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）
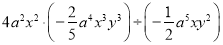
（2）704×696
（3）
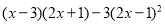
（4）
． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，纸上有5个边长为1的小正方形组成的纸片．可以用下面的方法把它剪拼成一个正方形．
（1）拼成的正方形的面积是多少，边长是多少．
（2）你能在3×3的正方形方格图3中，连接四个点组成面积为5的正方形吗？
（3）如图4，你能把这十个小正方形组成的图形纸，剪开并拼成一个大正方形吗？若能，请画出示意图，并写出边长为多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下列证明：
如图，已知AD⊥BC，EF⊥BC，∠1=∠2．
求证：DG∥BA．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠EFB=∠ADB=90°（ ）
∴EF∥AD（ ）
∴∠1=∠BAD（ ）
又∵∠1=∠2（已知）
∴ （等量代换）
∴DG∥BA．（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图：AD∥BC，E、F分别在DC、AB延长线上.∠DCB=∠DAB，AE⊥EF，∠DEA=30°.
（1）求证：DC//AB.
（2）求∠AFE的大小
-
科目： 来源： 题型：
查看答案和解析>>【题目】下表是橘子的销售额随橘子卖出质量的变化表：
质量/千克
1
2
3
4
5
6
7
8
9
…
销售额/元
2
4
6
8
10
12
14
16
18
…
（1）这个表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）当橘子卖出5千克时，销售额是_______元.
（3）如果用
表示橘子卖出的质量，
表示销售额，按表中给出的关系，与之间的关系式为______.（4）当橘子的销售额是100元时，共卖出多少千克橘子？
-
科目： 来源： 题型：
查看答案和解析>>【题目】由5个大小相同的小正方体拼成的几何体如图所示，则下列说法正确的是（ ）
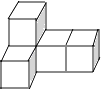
A.主视图的面积最小
B.左视图的面积最小
C.俯视图的面积最
D.三个视图的面积相等
相关试题
