【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A,B两点,且点A的横坐标为4,
(k>0)交于A,B两点,且点A的横坐标为4,

(1)求 k的值;
(2)利用图形直接写出不等式![]() x>
x>![]() 的解;
的解;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P,Q两点(P点在第一象限),若由点 A,B,P,Q为顶点组成的四边形面积为 24,求点 P的坐标.
(k>0)于P,Q两点(P点在第一象限),若由点 A,B,P,Q为顶点组成的四边形面积为 24,求点 P的坐标.
参考答案:
【答案】(1)8;(2)﹣4<x<0和x>4.(3)点P的坐标为(8,1)或(2,4).
【解析】(1)因为点A在直线y=![]() x上,故将其横坐标代入直线的解析式,求出对应的y的值,即可求得点A的坐标,再利用反比例函数图象上点的坐标特征即可求出k值;
x上,故将其横坐标代入直线的解析式,求出对应的y的值,即可求得点A的坐标,再利用反比例函数图象上点的坐标特征即可求出k值;
(2)根据两函数图象的上下位置关系即可得出不等式的解集;
(3)作AM⊥x轴于点M,PN⊥x轴于点N.设P点的坐标为(a,8a),根据正比例函数与反比例函数的对称性即可得出四边形APBQ为平行四边形,结合四边形面积为24以及三角形的面积公式即可得出关于a的一元二次方程,解方程即可得出a值,将其代入点P的坐标中即可得出结论.
(1)∵直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A,B两点,且点A的横坐标为 4,
(k>0)交于A,B两点,且点A的横坐标为 4,
∴![]() ×4=2,即:A点的坐标为(4,2),
×4=2,即:A点的坐标为(4,2),
∴k=4×2=8, 即:k的值为 8.
(2)∵点 A与点 B关于原点 O对称,
∴点B的坐标为(﹣4,﹣2),
又∵不等式![]() x>
x>![]() 的解,是函数图象上直线位于双曲线上方的部分对应的x的取值,
的解,是函数图象上直线位于双曲线上方的部分对应的x的取值,
∴由图象可知:不等式 ![]() x>
x>![]() 的解是:﹣4<x<0和x>4.
的解是:﹣4<x<0和x>4.
(3)作AM⊥x轴于点M,PN⊥x轴于点N.设P点的坐标为(a,![]() ).
).
∵P、Q 关于 O 点对称,A、B 关于 O 点对称,
∴四边形 APBQ 为平行四边形,
∴4S△OAP=24
∴S△OAP=6.
①当点 P 在直线 AB 的下方时,如图 1 所示,
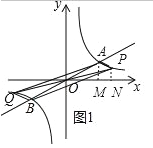
S△OAP=![]() ×4×2+
×4×2+![]() (
(![]() +2)(a﹣4)﹣
+2)(a﹣4)﹣![]() a
a![]() =6,
=6,
∴a2﹣6a﹣16=0,
解得:a1=﹣2,a2=8,
∴此时点P的坐标为(8,1);
②当点 P 在直线 AB 的上方时,如图 2 所示,
S△OAP=![]() a
a![]() +
+![]() (
(![]() +2)(4﹣a)﹣
+2)(4﹣a)﹣![]() ×4×2=6,
×4×2=6,
∴a2+6a﹣16=0,
解得:a1=2,a2=﹣8,
∴此时点P的坐标为(2,4).
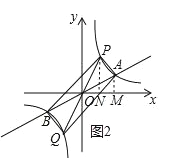
综上所述:点P的坐标为(8,1)或(2,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )
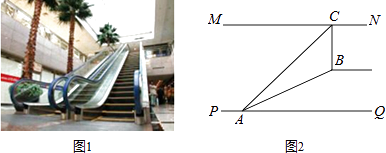
A.10.8米
B.8.9米
C.8.0米
D.5.8米 -
科目: 来源: 题型:
查看答案和解析>>【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB=
 ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为 .
.【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=
 AB;
AB;(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的不等式组
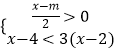 的解集为x>1,且关于x的分式方程
的解集为x>1,且关于x的分式方程 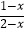 +
+ 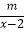 =3有非负整数解,则符合条件的m的所有值的和是( )
=3有非负整数解,则符合条件的m的所有值的和是( )
A.﹣2
B.﹣4
C.﹣7
D.﹣8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3
 ,BG=4,则GH的长为 .
,BG=4,则GH的长为 . 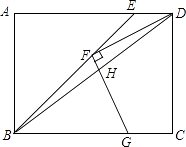
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1) 5(x+8)=6(2x-7)+5;
(2) 5-
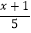 =x;
=x;(3)
 -
-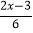 =1;
=1; (4)
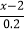 -
-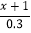 =1;
=1;(5) 2x-
 [x-
[x- (x-1)]=
(x-1)]= ( x-1).
( x-1). -
科目: 来源: 题型:
查看答案和解析>>【题目】为增强居民节约用水意识,某市在2018年开始对供水范围内的居民用水实行“阶梯收费”,具体收费标准如下表:

某户居民四月份用水10 m3时,缴纳水费23元.
(1) 求a的值;
(2) 若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
相关试题

