【题目】如果关于x的不等式组 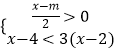 的解集为x>1,且关于x的分式方程
的解集为x>1,且关于x的分式方程 ![]() +
+ ![]() =3有非负整数解,则符合条件的m的所有值的和是( )
=3有非负整数解,则符合条件的m的所有值的和是( )
A.﹣2
B.﹣4
C.﹣7
D.﹣8
参考答案:
【答案】C
【解析】解: 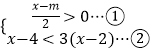 , 解①得x>m,
, 解①得x>m,
解②得x>1.
不等式组的解集是x>1,则m≤1.
解方程 ![]() +
+ ![]() =3,
=3,
去分母,得1﹣x﹣m=3(2﹣x),
去括号,得1﹣x﹣m=6﹣3x,
移项,得﹣x+3x=6﹣1+m,
合并同类项,得2x=5+m,
系数化成1得x= ![]() .
.
∵分式方程 ![]() +
+ ![]() =3有非负整数解,
=3有非负整数解,
∴5+m≥0,
∴m>﹣5,
∴﹣5≤m≤1,
∴m=﹣5,﹣3,0,1,
∴符合条件的m的所有值的和是﹣7,
故选C.
【考点精析】认真审题,首先需要了解分式方程的解(分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解),还要掌握一元一次不等式组的解法(解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论:w
①若a+b+c=0,且abc≠0,则方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,则a≠b;
③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=﹣
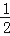 ;
;④若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解;
其中结论正确个数有( )
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )
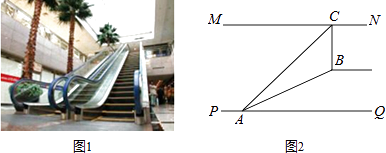
A.10.8米
B.8.9米
C.8.0米
D.5.8米 -
科目: 来源: 题型:
查看答案和解析>>【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB=
 ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为 .
.【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=
 AB;
AB;(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x与双曲线y=
x与双曲线y= (k>0)交于A,B两点,且点A的横坐标为4,
(k>0)交于A,B两点,且点A的横坐标为4,
(1)求 k的值;
(2)利用图形直接写出不等式
 x>
x> 的解;
的解;(3)过原点O的另一条直线l交双曲线y=
 (k>0)于P,Q两点(P点在第一象限),若由点 A,B,P,Q为顶点组成的四边形面积为 24,求点 P的坐标.
(k>0)于P,Q两点(P点在第一象限),若由点 A,B,P,Q为顶点组成的四边形面积为 24,求点 P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3
 ,BG=4,则GH的长为 .
,BG=4,则GH的长为 . 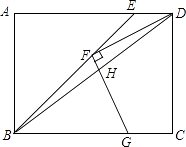
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1) 5(x+8)=6(2x-7)+5;
(2) 5-
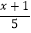 =x;
=x;(3)
 -
-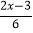 =1;
=1; (4)
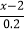 -
-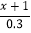 =1;
=1;(5) 2x-
 [x-
[x- (x-1)]=
(x-1)]= ( x-1).
( x-1).
相关试题

