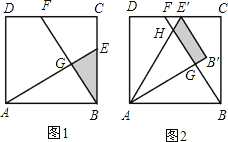
【题目】已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
参考答案:
【答案】(1)证明见解析;
(2)![]() ;
;
(3)没有变化,理由见解析.
【解析】试题分析:(1)由四边形ABCD是正方形,可得∠ABE=∠BCF=90°,AB=BC,又由AE⊥BF,由同角的余角相等,即可证得∠BAE=∠CBF,然后利用ASA,即可判定:△ABE≌△BCF;
(2)由正方形ABCD的面积等于3,即可求得此正方形的边长,由在△BGE与△ABE中,∠GBE=∠BAE,∠EGB=∠EBA=90°,可证得△BGE∽△ABE,由相似三角形的面积比等于相似比的平方,即可求得答案;
(3)首先由正切函数,求得∠BAE=30°,易证得Rt△ABE≌Rt△AB′E′≌Rt△ADE′,可得DE’=B’E’=BE,由(1)可知BE=CF,从而得CF=DE’,继而可得DF=CE’;
试题解析:(1)正方形ABCD中,AB=BC,∠ABC=∠BCF=90°,∴∠ABF+∠CBF=90°, ∵AE⊥BF, ∴∠ABF+∠BAE=90°,∴∠CBF=∠BAE ,∴△ABE ≌△BCF ;
(2)∵正方形面积为3,∴AB=![]() ,∵∠GBE=∠BAE,∠EGB=∠EBA=90°,∴△BGE∽△ABE,∴
,∵∠GBE=∠BAE,∠EGB=∠EBA=90°,∴△BGE∽△ABE,∴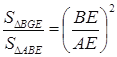 ,又∵BE=1,∴AE2=AB2+BE2=3+1=4,∴S△BGE=
,又∵BE=1,∴AE2=AB2+BE2=3+1=4,∴S△BGE=![]() =
=![]() ;
;
(3) ∵BE=1,AB=![]() ,∴tan∠BAE=
,∴tan∠BAE=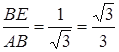 ,∴∠BAE=30°,由已知易证得Rt△ABE≌Rt△AB′E′≌Rt△ADE′,∴DE’=B’E’=BE,∵△ABE≌△BCF,∴BE=CF,∴CF=DE’,∴DF=CE′;
,∴∠BAE=30°,由已知易证得Rt△ABE≌Rt△AB′E′≌Rt△ADE′,∴DE’=B’E’=BE,∵△ABE≌△BCF,∴BE=CF,∴CF=DE’,∴DF=CE′;
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x﹣1=x2﹣1的根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式﹣6y4+5xy3﹣4x2+x3y是按( )
A.x的降幂排列
B.x的升幂排列
C.y的降幂排列
D.y的升幂排列 -
科目: 来源: 题型:
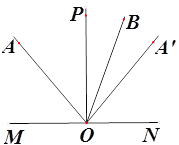
查看答案和解析>>【题目】如图,平面内一定点A在直线MN的上方,点O为直线MN上一动点 ,作射线OA、OP、OA’,当点O在直线MN上运动时,始终保持∠MOP=90°、∠AOP=∠A’OP,将射线OA绕点O顺时针旋转60°得到射线OB
(1)如图,当点O运动到使点A在射线OP的左侧,若OB平分∠A’OP,求∠AOP的度数;
(2)当点O运动到使点A在射线OP的左侧,∠AOM=3∠A’OB时,求
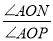 的值;
的值;(3)当点O运动到某一时刻时,∠A’OB=150°,直接写出∠BOP= 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在3×3方格上做填字游戏,要求每行每列及对角线上三个方格中的数字和都等于S,又填在图中三格中的数字如图,若要能填成,则( )
10
8 13
A.S=24 B.S=30 C.S=31 D.S=39
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )

A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB∥DC,AD=BC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )

A.10
B.12
C.16
D.18
相关试题

