【题目】如图,在平面直角坐标系中,点![]() ,为
,为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,其中
轴正半轴上一点,其中![]() 满足方程
满足方程![]() .
.
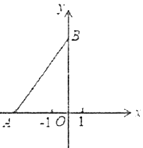
(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)点![]() 为
为![]() 轴负半轴上一点,且
轴负半轴上一点,且![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半,若存在,求出相应的
的面积的一半,若存在,求出相应的![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)点A坐标为(-3,0),点B坐标为(0,4);(2)点C坐标为(0,-4);(3)存在,点P坐标为(![]() ,0)或(-
,0)或(-![]() ,0).
,0).
【解析】
(1)解方程![]() 可求出b的值,即可得A、B坐标;
可求出b的值,即可得A、B坐标;
(2)根据A、B坐标可得OA、OB的长,利用三角形面积公式可求出BC的长,根据点C在y轴负半轴可得OC的长,可得C点坐标;
(3)利用三角形面积公式可求出OP的长,分点P在原点左边和右边两种情况,求出OP的坐标即可.
(1)∵![]() ,
,
∴b=1,
∵![]() ,
,![]() ,
,
∴点A坐标为(-3,0),点B坐标为(0,4).
(2)如图,∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∵△ABC的面积为12,
∴![]() BC·OA=12,即
BC·OA=12,即![]() ×3×BC=12,
×3×BC=12,
解得:BC=8,
∵点![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点,
∴OC=BC-OB=8-4=4,
∴点C坐标为(0,-4).
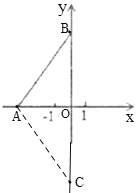
(3)如图,∵![]() 的面积等于
的面积等于![]() 的面积的一半,△ABC的面积为12,
的面积的一半,△ABC的面积为12,
∴△PBC的面积为6,
∴![]() BC·OP=6,即
BC·OP=6,即![]() ×8×OP=6,
×8×OP=6,
解得:OP=![]() ,
,
当点P在原点左边时,点P坐标为(-![]() ,0),
,0),
当点P在原点右边时,点P坐标为(![]() ,0),
,0),

∴存在一点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半,点P坐标为(
的面积的一半,点P坐标为(![]() ,0)或(-
,0)或(-![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为a,射线AM是∠A外角的平分线,点E在边AB上运动(不与点A、B重合),点F在射线AM上,且AF=√2BE,CF与AD相交于点G,连结EC、EF、EG.
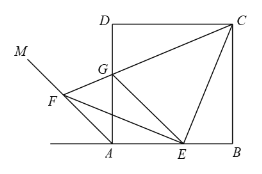
(1)求证:CE=EF;
(2)求△AEG的周长(用含a的代数式表示)
(3)试探索:点E在边AB上运动至什么位置时,△EAF的面积最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中,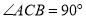 ,
,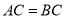 ,直线
,直线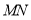 经过点
经过点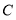 ,且
,且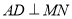 于点
于点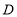 ,
,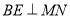 于点
于点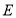 .
.
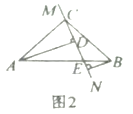
(1)当直线
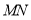 绕点
绕点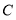 旋转到图1的位置时,求证:
旋转到图1的位置时,求证:①
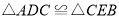 ;
;②
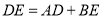 .
.(2)当直线
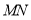 绕点
绕点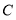 旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由.
旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由. -
科目: 来源: 题型:
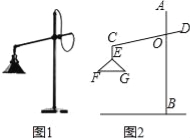
查看答案和解析>>【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,地面上小山的两侧有
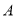 ,
,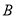 两地,为了测量
两地,为了测量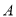 ,
,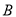 两地的距离,让一热气球从小山西侧
两地的距离,让一热气球从小山西侧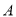 地出发沿与
地出发沿与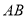 成
成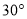 角的方向,以每分钟
角的方向,以每分钟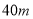 的速度直线飞行,
的速度直线飞行,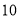 分钟后到达
分钟后到达 处,此时热气球上的人测得
处,此时热气球上的人测得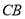 与
与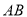 成
成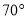 角,请你用测得的数据求
角,请你用测得的数据求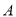 ,
,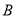 两地的距离
两地的距离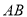 长.(结果用含非特殊角的三角函数和根式表示即可)
长.(结果用含非特殊角的三角函数和根式表示即可)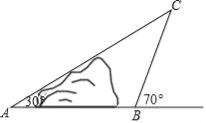
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E为BC上一点,连接AE,作EF⊥AE交AB于F.
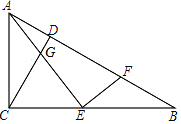
(1)求证:△AGC∽△EFB.
(2)除(1)中相似三角形,图中还有其它相似三角形吗?如果有,请把它们都写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
相关试题

