【题目】已知抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点.
(1)求m的取值范围;
(2)当m取满足条件的最大整数时,求抛物线与x轴有两个交点的坐标.
参考答案:
【答案】
(1)解:∵抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点,
∴y=0时,(m﹣2)x2+2mx+m+3=0,则△=(2m)2﹣4×(m﹣2)×(m+3)>0,m﹣2≠0,
解得m<6且m≠2.
即m的取值范围是:m<6且m≠2
(2)解:∵m<6且m≠2,
∴m满足条件的最大整数是m=5.
∴y=3x2+10x+8.
当y=0时,3x2+10x+8=0.
解得 ![]() .
.
即抛物线与x轴有两个交点的坐标是:(﹣2,0),( ![]() ,0)
,0)
【解析】(1)根据抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点时,可知(m﹣2)x2+2mx+m+3=0时,△>0且m﹣2≠0,从而可以解答本题;(2)根据第一问求得的m的取值范围,可以得到m的最大整数,从而可以求得抛物线与x轴有两个交点的坐标.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:在数学课上,老师提出如下问题:
尺规作图,过圆外一点作圆的切线.
已知:⊙O和点P
求过点P的⊙O的切线小涵的主要作法如下:
如图,(1)连结OP,作线段OP的中点A;
(2)以A为圆心,OA长为半径作圆,交⊙O于点B,C;
(3)作直线PB和PC.
所以PB和PC就是所求的切线.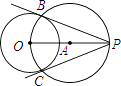
老师说:“小涵的做法是正确的.”
请回答:小涵的作图依据是 .
-
科目: 来源: 题型:
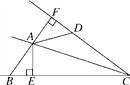
查看答案和解析>>【题目】如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.
(1)若∠ABE=60°,求∠CDA的度数;
(2)若AE=2,BE=1,CD=4.求四边形AECD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )

A. 4次 B. 3次 C. 2次 D. 1次
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:

(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1.
(2)作△ABC关于坐标原点成中心对称的△A2B2C2.
(3)求B1的坐标 C2的坐标 .
-
科目: 来源: 题型:
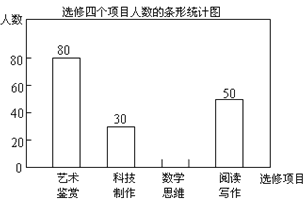
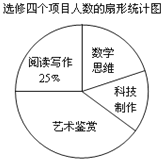
查看答案和解析>>【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图:
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了___名学生,扇形统计图中“艺术鉴赏”部分的圆心角是___度;
(2)此次调查“数学思维”的人数为_________,并补充完整条形图;
(3)现该校共有600名学生报名参加这四个选修项目,请你估计其中有____名学生选修“科技制作”项目.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,它们除颜色外都相同。
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率不小于
 ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
相关试题

