搜索
【题目】如图，在平面直角坐标系中，直线y＝2x+4分别交x轴，y轴于点A，C，点D（m，2）在直线AC上，点B在x轴正半轴上，且OB＝3OC．点E是y轴上任意一点记点E为（0，n）．
（1）求直线BC的关系式；
（2）连结DE，将线段DE绕点D按顺时针旋转90°得线段DG，作正方形DEFG，是否存在n的值，使正方形DEFG的顶点F落在△ABC的边上？若存在，求出所有的n值并直接写出此时正方形DEFG与△ABC重叠部分的面积；若不存在，请说明理由．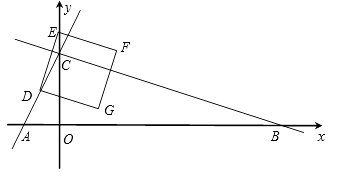
参考答案：
【答案】
（1）
解：求出直线BC关系式为y=
x+4.
（2）
解：当F在BC边上时求得n=
，S重叠=
，
当F在AB边上时求得n=1，S重叠=
，
当F在AC边上时显然不合题意，舍去.
【解析】（1）利用直线y＝2x+4分别交x轴，y轴于点A，C，可求出点C的坐标，再根据OB＝3OC．可求出点B的坐标，进而利用待定系数法就可求出直线BC关系式.
（2）此问注意分情况讨论：①当F在BC边上时；②当F在AB边上时；③当F在AC边上时三种情况，分别计算即可.但注意第三种情况，明显不合题意.
-
科目： 来源： 题型：
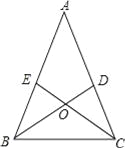
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E，某同学分析图形后得出以下结论，上述结论一定正确的是______（填代号）．
①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△BCE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“夕阳红”养老院共有普通床位和高档床位共500张．已知今年一月份入住普通床位老人300人，入住高档床位老人90人，共计收费51万元；今年二月份入住普通床位老人350人，入住高档床位老人100人，共计收费58万元．
（1）求普通床位和高档床位每月收费各多少元？
（2）根据国家养老政策规定，为保障普通居民的养老权益，所有实际入住高档床位数不得超过普通床位数的三分之一；另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴．经测算，该养老院普通床位的运营成本是每月1200元/张，入住率为90%；高档床位的运营成本是每月2000元/张，入住率为70%．问该养老院应该怎样安排500张床的普通床位和高档床位数量，才能使每月的利润最大，最大为多少元？（月利润＝月收费－月成本+月补贴） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线
（其中 
）与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，抛物线的对称轴l与x轴交于点D，且点D恰好在线段BC的垂直平分线上．
（1）求抛物线的关系式；
（2）过点
的线段MN∥y轴，与BC交于点P，与抛物线交于点N．若点E是直线l上一点，且∠BED＝∠MNB－∠ACO时，求点E的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，每个小立方体的棱长为1，图1中共有1个立方体，其中1个看得见，0个看不见；图2中共有8个小立方体，其中7个看得见，1个看不见；图3中共有27个小立方体，其中19个看得见，8个看不见；……；则第10个图形中，其中看得见的小立方体个数是（ ）
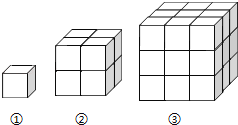
A. 270 B. 271 C. 272 D. 273
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平整的地面上，有若干个完全相同的棱长为1cm的小正方体堆成一个几何体，如图所示：
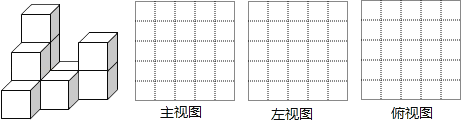
（1）这个几何体是由 个小正方体组成，请画出这个几何体的三视图；
（2）如果在这个几何体露在外面的表面喷上黄色的漆，每平方厘米用2克，则共需 克
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，AC=BC=AD．
（1）作∠A的平分线交CD于E；
（2）过B作CD的垂线，垂足为F；
（3）请写出图中两对全等三角形（不添加任何字母），并选择其中一对加以证明．
相关试题
