【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心____点,按顺时针方向旋转___度得到;
(3)若BC=8,DE=2,求△AEF的面积.

参考答案:
【答案】 (1)见解析;(2)A,90;(3) 34.
【解析】
(1)根据正方形的性质得![]() ,
,![]() ,然后利用“
,然后利用“![]() ”易证得
”易证得![]() ;
;
(2)由于![]() 得
得![]() ,则
,则![]() ,即
,即![]() ,根据旋转的定义可得到
,根据旋转的定义可得到![]() 可以由
可以由![]() 绕旋转中心
绕旋转中心![]() 点,按顺时针方向旋转
点,按顺时针方向旋转![]() 得到;
得到;
(3)先利用勾股定理可计算出![]() ,再根据
,再根据![]() 可以由
可以由![]() 绕旋转中心
绕旋转中心![]() 点,按顺时针方向旋转
点,按顺时针方向旋转![]() 得到
得到![]() ,
,![]() ,然后根据直角三角形的面积公式计算即可.
,然后根据直角三角形的面积公式计算即可.
解:(1)∵四边形ABCD是正方形,∴AD=AB,∠D=∠ABC=90°,
而F是CB的延长线上的点,∴∠ABF=∠D=90°.
又∵AB=AD,DE=BF,∴△ADE≌△ABF(SAS);
(2)![]()
![]() ,
,
![]()
![]()
而![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]()
![]() 可以由
可以由![]() 绕旋转中心
绕旋转中心![]() 点,按顺时针方向旋转
点,按顺时针方向旋转![]() 得到.
得到.
故答案为:![]() 、
、![]() .
.
(3)∵BC=8,∴AD=8,在Rt△ADE中,DE=2,AD=8,
∴AE=![]() =2
=2![]() ,
,
∵△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90°得到,
∴AE=AF,∠EAF=90°.∴△AEF的面积=AE2=×4×17=34.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且与EF交于点O,那么与∠AOE相等的角有( )
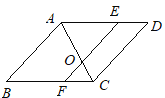
A. 6个B. 5个C. 4个D. 3个
-
科目: 来源: 题型:
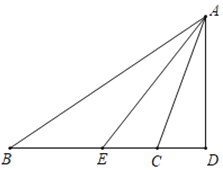
查看答案和解析>>【题目】如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B2,C2的坐标;
(3)若点P(a,b)是△ABC内任意一点,试写出将△ABC绕点O逆时针旋转90°后点P的对应点P2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=_____.
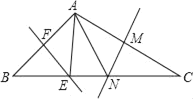
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC≌△DEF,点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
相关试题

