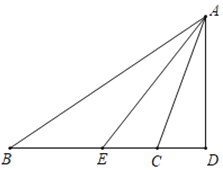
【题目】如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD.
参考答案:
【答案】(1)![]() ,(2)
,(2)![]() .
.
【解析】
(1)根据垂直的定义得到∠D=90°,根据邻补角的定义得到∠ACD![]() ,根据三角形的内角和得到∠BAC=50°,根据角平分线的定义得到∠CAE
,根据三角形的内角和得到∠BAC=50°,根据角平分线的定义得到∠CAE![]() ∠BAC=25°,于是得到结论; (2)根据垂直的定义得到∠D=90°,得到∠ACD=
∠BAC=25°,于是得到结论; (2)根据垂直的定义得到∠D=90°,得到∠ACD=![]() ,求得∠BAC
,求得∠BAC![]() ,根据角平分线的定义得到∠CAE
,根据角平分线的定义得到∠CAE![]() ∠BAC
∠BAC![]() ,根据角的和差即可得到结论.
,根据角的和差即可得到结论.
解:(1)∵AD⊥BC, ∴∠D=90°,
∵∠ACB=100°, ∴∠ACD![]() ,
,
∴∠CAD=![]() , ∵∠B=30°,
, ∵∠B=30°,
∴∠BAD![]() , ∴∠BAC=50°,
, ∴∠BAC=50°,
∵AE平分∠BAC, ∴∠CAE![]() ∠BAC=25°,
∠BAC=25°,
∴∠EAD=∠CAE+∠CAD=35°;
(2)∵AD⊥BC, ∴∠D=90°,
∵∠ACB=β, ∴∠ACD=![]() ,
,
∴∠CAD![]() ,
,
∵∠B=α, ∴∠BAD=![]() ,
,
∴∠BAC![]() ,
,
∵AE平分∠BAC, ∴∠CAE![]() ∠BAC
∠BAC![]() ,
,
∴∠EAD=∠CAE+∠CAD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则
①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且与EF交于点O,那么与∠AOE相等的角有( )
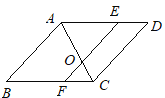
A. 6个B. 5个C. 4个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B2,C2的坐标;
(3)若点P(a,b)是△ABC内任意一点,试写出将△ABC绕点O逆时针旋转90°后点P的对应点P2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心____点,按顺时针方向旋转___度得到;
(3)若BC=8,DE=2,求△AEF的面积.

-
科目: 来源: 题型:
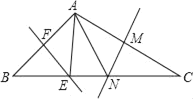
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=_____.
相关试题

