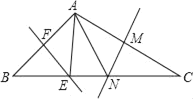
【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=_____.
参考答案:
【答案】32°
【解析】
先由∠BAC=106°及三角形内角和定理求出∠B+∠C的度数,再根据线段垂直平分线的性质求出∠B=∠BAE,∠C=∠CAN,即∠B+∠C=∠BAE+∠CAN,由∠EAN=∠BAC(∠BAE+∠CAN)解答即可.
解:在△ABC中,∠BAC=106°,
∴∠B+∠C=180°∠BAC=180°106°=74°,
∵EF、MN分别是AB、AC的中垂线,
∴∠B=∠BAE,∠C=∠CAN,
即∠B+∠C=∠BAE+∠CAN=74°,
∴∠EAN=∠BAC(∠BAE+∠CAN)=106°74°=32°.
故答案为32°.
-
科目: 来源: 题型:
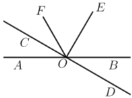
查看答案和解析>>【题目】如图,直线
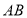 、
、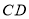 相交于点
相交于点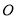 ,
,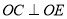 ,
,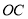 平分
平分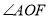 ,
,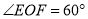 .
.
(1)求
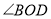 的大小,根据下列解答填空(理由或数学式)
的大小,根据下列解答填空(理由或数学式)解:∵
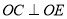 (已知),
(已知),∴
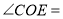 ______°,
______°,∵
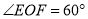 ,
,∴
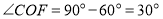 .
.∵
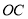 平分
平分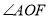 (已知),
(已知),∴
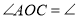 ______
______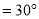 .
.∵
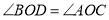 (______),
(______),∴
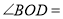 ______°.
______°.(2)直接写出图中所有与
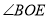 互余的角.
互余的角. -
科目: 来源: 题型:
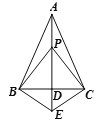
查看答案和解析>>【题目】如图,已知AB=AC,BE=CE,下面四个结论:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正确的结论个数有( )个.
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.

(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=
 ,AD=6,求线段AE的长.
,AD=6,求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列各题.
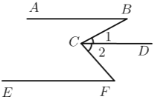
(1)探究:如图,
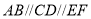 ,试说明
,试说明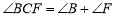 .
.
(2)拓展:如图,
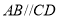 ,
,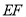 与
与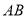 交于点
交于点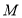 ,
,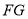 与
与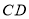 交于点
交于点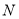 .若
.若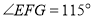 ,
,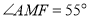 ,利用探究结论求
,利用探究结论求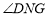 的度数.
的度数.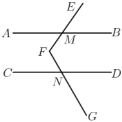
(3)应用:如图,
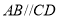 ,点
,点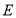 在
在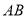 上,点
上,点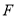 在
在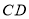 上,点
上,点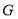 、
、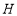 在
在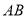 与
与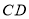 之间,
之间,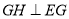 于点
于点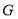 .若
.若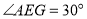 ,
,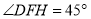 ,则
,则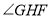 的大小为______度.
的大小为______度.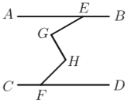
-
科目: 来源: 题型:
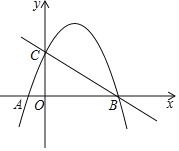
查看答案和解析>>【题目】抛物线
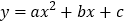 经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).(1)求抛物线的表达式;
(2)点P为直线BC上方抛物线的一点,分别连接PB、PC,若直线BC恰好平分四边形COBP的面积,求P点坐标;
(3)在(2)的条件下,是否在该抛物线上存在一点Q,该抛物线对称轴上存在一点N,使得以A、P、Q、N为顶点的四边形为平行四边形?若存在,求出Q点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况(如下图),进行整理后,绘制了如下两幅尚不完整的统计图:
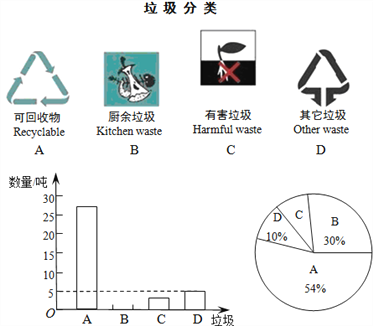
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图中,求出“D”部分所对应的圆心角等于 度;
(3)在抽样数据中,产生的有害垃圾共有 吨;
(4)调查发现,在可回收物中废纸垃圾约占
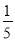 ,若每回收1吨废纸可再造纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造纸多少吨?
,若每回收1吨废纸可再造纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造纸多少吨?
相关试题

