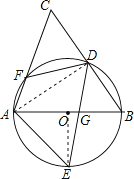
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB= ![]() ,E是
,E是 ![]() 的中点,求EGED的值.
的中点,求EGED的值.
参考答案:
【答案】
(1)
证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(2)
解:∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°-∠E,
又∵∠CFD=180°-∠AFD,
∴∠CFD=∠E=55°,
又∵∠E=∠C=55°,
∴∠BDF=∠C+∠CFD=110°;
(3)
解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB= ![]() ,BD=4,
,BD=4,
∴AB=6,
∵E是 ![]() 的中点,AB是⊙O的直径,
的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3 ![]() ,
,
∵E是 ![]() 的中点,
的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴ ![]() ,
,
即EGED=AE2=18.
【解析】(1)直接利用圆周角定理得出AD⊥BC,劲儿利用线段垂直平分线的性质得出AB=AC,即可得出∠E=∠C;(2)利用圆内接四边形的性质得出∠AFD=180°﹣∠E,进而得出∠BDF=∠C+∠CFD,即可得出答案;(3)根据cosB= ![]() ,得出AB的长,再求出AE的长,进而得出△AEG∽△DEA,求出答案即可.此题主要考查了圆的综合题、圆周角定理以及相似三角形的判定与性质以及圆内接四边形的性质等知识,根据题意得出AE,AB的长是解题关键.
,得出AB的长,再求出AE的长,进而得出△AEG∽△DEA,求出答案即可.此题主要考查了圆的综合题、圆周角定理以及相似三角形的判定与性质以及圆内接四边形的性质等知识,根据题意得出AE,AB的长是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=
 (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式. 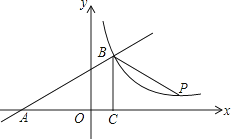
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10 ,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
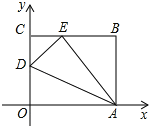
(1)求CE和OD的长;
(2)求直线DE的表达式;
(3)直线y=kx+b与DE平行,当它与矩形OABC有公共点时,直接写出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b互为相反数,c、d互为倒数,|x|=2018,求2a+2b+
 +cdx的值.
+cdx的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<
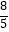 ).
). 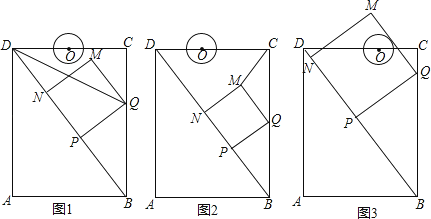
(1)如图1,连接DQ平分∠BDC时,t的值为;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.

(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2 , 当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,BE与CF交于点D,则对于下列结论:
,BE与CF交于点D,则对于下列结论: ≌
≌ ;
; ≌
≌ ;
; ≌
≌ ;
; 在
在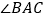 的平分线上
的平分线上 其中正确的是( )
其中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
相关试题

