【题目】如图,直线y=kx+b(k≠0)与两坐标轴分别交于点B,C,点A的坐标为(-2,0)点D的坐标为(1,0)
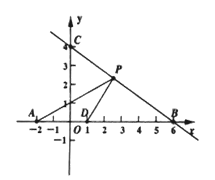
(1)试确定直线BC的函数关系式.
(2)若p(x,y)是直线BC在第一象限内的一个动点,试写出△ADP的面积S与x的函数关系式.
(3)当P运动到什么位置时,△ADP的面积为3?请写出此时点P的坐标,并说明理由.
参考答案:
【答案】(1)y=-![]() x+4;(2) S=-x+6;(3) (3,2)
x+4;(2) S=-x+6;(3) (3,2)
【解析】(1)运用待定系数法即可求出解析式;
(2)利用三角形面积公式即可建立函数关系式;
(3)利用(2)中的函数关系式即可得出答案.
解:(1)设直线BC的函数关系式为y=kx+b(k≠0),
由题意,得方程组,![]() ,
,
解得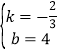 ,
,
所以,函数y与x的函数关系式为y=-![]() x+4;
x+4;
(2)由题意,P(x,y)是直线BC在第一象限的点,
∴y>0,且y=-![]() x+4,
x+4,
又,点A的坐标为(-2,0),点D的坐标为(1,0),
∴AD=3,
∴S△ADP=![]() ×3×〔-
×3×〔-![]() x+4 〕=-x+6,
x+4 〕=-x+6,
即S=-x+6;
(3)当S=3时,
-x+6=3,
解得x=3,
所以y=-![]() ×3+4=2,
×3+4=2,
此时,点P的坐标为(3,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
 是线段
是线段 所在平面内任意一点,分别以
所在平面内任意一点,分别以 、
、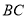 为边,在
为边,在 同侧作等边
同侧作等边 和等边
和等边 ,联结
,联结 、
、 交于点
交于点 .
.(1)如图1,当点
 在线段
在线段 上移动时,线段
上移动时,线段 与
与 的数量关系是:________;
的数量关系是:________;(2)如图2,当点
 在直线
在直线 外,且
外,且 ,仍分别以
,仍分别以 、
、 为边,在
为边,在 同侧作等边
同侧作等边 和等边
和等边 ,联结
,联结 、
、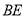 交于点
交于点 .(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时
.(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时 是否随
是否随 的大小发生变化?若变化,写出变化规律,若不变,请求出
的大小发生变化?若变化,写出变化规律,若不变,请求出 的度数;
的度数;(3)如图3,在(2)的条件下,联结
 ,求证:
,求证:  平分
平分 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要

求画图:
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形ABC;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方
形,这个正方形的面积= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2= 17, 且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
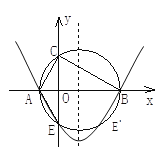
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=2x2-kx-1与x轴两交点的横坐标,一个大于2,另一个小于2,试求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于任意两点A(x1,y1)B (x2,y2),规定运算:
(1)A⊕B=(x1+x2,y1+y2);
(2)A⊙B=x1x2+y1y2;
(3)当x1=x2且y1=y2时,A=B.
有下列四个命题:
①若有A(1,2),B(2,﹣1),则A⊕B=(3,1),A⊙B=0;
②若有A⊕B=B⊕C,则A=C;
③若有A⊙B=B⊙C,则A=C;
④(A⊕B)⊕C=A⊕(B⊕C)对任意点A、B、C均成立.
其中正确的命题为______(只填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD的边AB=3,AD=2,将此矩形置入直角坐标系中,使AB在x 轴上,点C 在直线y=x-2上.
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.

相关试题

