【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

参考答案:
【答案】(1)![]() ;(2)x>1;(3)P(﹣
;(2)x>1;(3)P(﹣![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)求得A(1,3),把A(1,3)代入双曲线y=![]() ,可得y与x之间的函数关系式;
,可得y与x之间的函数关系式;
(2)依据A(1,3),可得当x>0时,不等式![]() x+b>
x+b>![]() 的解集为x>1;
的解集为x>1;
(3)分两种情况进行讨论,AP把△ABC的面积分成1:3两部分,则CP=![]() BC=
BC=![]() ,或BP=
,或BP=![]() BC=
BC=![]() ,即可得到OP=3﹣
,即可得到OP=3﹣![]() =
=![]() ,或OP=4﹣
,或OP=4﹣![]() =
=![]() ,进而得出点P的坐标.
,进而得出点P的坐标.
(1)把A(1,m)代入y1=﹣x+4,可得m=﹣1+4=3,
∴A(1,3),
把A(1,3)代入双曲线y=![]() ,可得k=1×3=3,
,可得k=1×3=3,
∴y与x之间的函数关系式为:y=![]() ;
;
(2)∵A(1,3),
∴当x>0时,不等式![]() x+b>
x+b>![]() 的解集为:x>1;
的解集为:x>1;
(3)y1=﹣x+4,令y=0,则x=4,
∴点B的坐标为(4,0),
把A(1,3)代入y2=![]() x+b,可得3=
x+b,可得3=![]() +b,
+b,
∴b=![]() ,
,
∴y2=![]() x+
x+![]() ,
,
令y2=0,则x=﹣3,即C(﹣3,0),
∴BC=7,
∵AP把△ABC的面积分成1:3两部分,
∴CP=![]() BC=
BC=![]() ,或BP=
,或BP=![]() BC=
BC=![]()
∴OP=3﹣![]() =
=![]() ,或OP=4﹣
,或OP=4﹣![]() =
=![]() ,
,
∴P(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
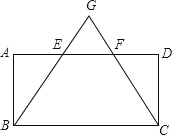
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G, GB=GC.
(1)求证:四边形ABCD是矩形;
(2)若△GEF的面积为2.
①求四边形BCFE的面积;
②四边形ABCD的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形的边长均为1的方格纸中有线段AB,其中点A、B均在小正方形的顶点上.
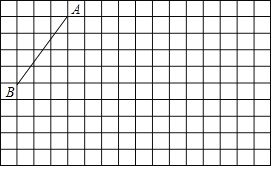
(1)在方格纸中画出以BC为底的钝角等腰三角形ABC,且点C在小正方形的顶点上;
(2)将(1)中的△ABC绕点C逆时针旋转90°得到△DEC(点A的对应点是点D,点B的对应点是点E),画出△CDE;
(3)在(2)的条件下,连接BE,请直接写出△BCE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:
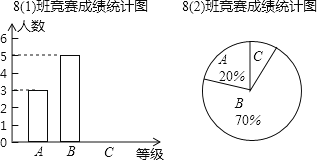
(1)求各班参赛人数,并补全条形统计图;
(2)此次竞赛中8(2)班成绩为C级的人数为_______人;
(3)小明同学根据以上信息制作了如下统计表:
平均数(分)
中位数(分)
方差
8(1)班
m
90
n
8(2)班
91
90
29
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与
OD的延长线交于点P,PC、AB的延长线交于点F.
(1)求证:PC是⊙O的切线;
(2)若∠ABC=60°,AB=10,求线段CF的长.

-
科目: 来源: 题型:
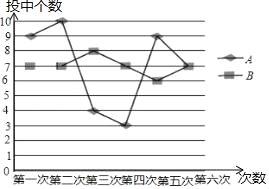
查看答案和解析>>【题目】某班为确定参加学校投篮比赛的任选,在A、B两位投篮高手间进行了6次投篮比赛,每人每次投10个球,将他们每次投中的个数绘制成如图所示的折线统计图.
(1)根据图中所给信息填写下表:
投中个数统计
平均数
中位数
众数
A
8
B
7
7
(2)如果这个班只能在A、B之间选派一名学生参赛,从投篮稳定性考虑应该选派谁?请你利用学过的统计量对问题进行分析说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在
 ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.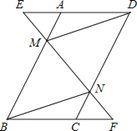
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
相关试题

