搜索
【题目】分解因式：18m2﹣32n2= ．
参考答案：
【答案】2（3m﹣4n）（3m+4n）
【解析】解：18m2﹣32n2=2（9m2﹣16n2）
=2（3m﹣4n）（3m+4n）．
所以答案是：2（3m﹣4n）（3m+4n）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．
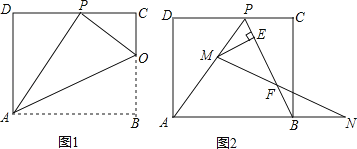
（1）如图1，已知折痕与边BC交于点O，连结AP、OP、OA．
①求证：△OCP∽△PDA；
②若△OCP与△PDA的面积比为1：4，求边AB的长；
（2）若图1中的点P恰好是CD边的中点，求∠OAB的度数；
（3）如图2，
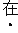
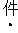
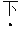，擦去折痕AO、线段OP，连结BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN=PM，连结MN交PB于点F，作ME⊥BP于点E．试问当点M、N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；若不变，求出线段EF的长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列等式中，正确的是（ ）
A. 3a﹣2a=1 B. a2a3=a5 C. （﹣2a3）2=﹣4a6 D. （a﹣b）2=a2﹣b2
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式
① -49a2bc-14ab2c+7ab
②(2a+b)(2a-3b)-8a(2a+b)
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
．下列结论：①△APD≌△AEB；②点B到直线AE的距离为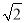
；③EB⊥ED；④S△APD+S△APB=1+
；⑤S正方形ABCD=4+．其中正确结论的序号是（ ）
A.①③④ B．①②⑤ C．③④⑤ D．①③⑤
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，四边形ABCD是等腰梯形，AD∥BC，AB=DC，BC在x轴上，点A在y轴的正半轴上，点A，D的坐标分别为A（0，2），D（2，2），AB=2
，连接AC．
（1）求出直线AC的函数解析式；
（2）求过点A，C，D的抛物线的函数解析式；
（3）在抛物线上有一点P（m，n）（n＜0），过点P作PM垂直于x轴，垂足为M，连接PC，使以点C，P，M为顶点的三角形与Rt△AOC相似，求出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】填在下面各正方形中的四个数之间都有一定的规律，据此规律得出a＋b＋c＝________．
相关试题
