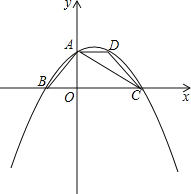
【题目】如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2![]() ,连接AC.
,连接AC.

(1)求出直线AC的函数解析式;
(2)求过点A,C,D的抛物线的函数解析式;
(3)在抛物线上有一点P(m,n)(n<0),过点P作PM垂直于x轴,垂足为M,连接PC,使以点C,P,M为顶点的三角形与Rt△AOC相似,求出点P的坐标.
参考答案:
【答案】(1)y=﹣![]() x+2;(2)y=﹣
x+2;(2)y=﹣![]() x2+
x2+![]() x+2;(3)点P的坐标为(﹣4,﹣4)或(﹣10,﹣28)或(6,﹣4).
x+2;(3)点P的坐标为(﹣4,﹣4)或(﹣10,﹣28)或(6,﹣4).
【解析】
试题分析:(1)先在Rt△ABO中,运用勾股定理求出OB=![]() =
=![]() =2,得出B(﹣2,0),再根据等腰梯形的对称性可得C点坐标为(4,0),又A(0,2),利用待定系数法即可求出直线AC的函数解析式;
=2,得出B(﹣2,0),再根据等腰梯形的对称性可得C点坐标为(4,0),又A(0,2),利用待定系数法即可求出直线AC的函数解析式;
(2)设所求抛物线的解析式为y=ax2+bx+c,将A,C,D三点的坐标代入,利用待定系数法即可求出抛物线的函数解析式;
(3)先由点P(m,n)(n<0)在抛物线y=﹣![]() x2+
x2+![]() x+2上,得出m<﹣2或m>4,n=﹣
x+2上,得出m<﹣2或m>4,n=﹣![]() m2+
m2+![]() m+2<0,于是PM=
m+2<0,于是PM=![]() m2﹣
m2﹣![]() m﹣2.由于∠PMC=∠AOC=90°,所以当Rt△PCM与Rt△AOC相似时,有
m﹣2.由于∠PMC=∠AOC=90°,所以当Rt△PCM与Rt△AOC相似时,有![]() =
=![]() =
=![]() 或
或![]() =
=![]() =2.再分两种情况进行讨论:①若m<﹣2,则MC=4﹣m.由
=2.再分两种情况进行讨论:①若m<﹣2,则MC=4﹣m.由![]() =
=![]() =
=![]() ,列出方程
,列出方程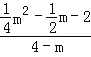 =
=![]() ,解方程求出m的值,得到点P的坐标为(﹣4,﹣4);由
,解方程求出m的值,得到点P的坐标为(﹣4,﹣4);由![]() =
=![]() =2,列出方程
=2,列出方程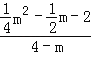 =2,解方程求出m的值,得到点P的坐标为(﹣10,﹣28);②若m>4,则MC=m﹣4.由
=2,解方程求出m的值,得到点P的坐标为(﹣10,﹣28);②若m>4,则MC=m﹣4.由![]() =
=![]() =
=![]() 时,列出方程
时,列出方程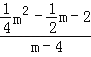 =
=![]() ,解方程求出m的值均不合题意舍去;由
,解方程求出m的值均不合题意舍去;由![]() =
=![]() =2,列出方程
=2,列出方程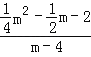 =2,解方程求出m的值,得到点P的坐标为(6,﹣4).
=2,解方程求出m的值,得到点P的坐标为(6,﹣4).
解:(1)由A(0,2)知OA=2,
在Rt△ABO中,∵∠AOB=90°,AB=2![]() ,
,
∴OB=![]() =
=![]() =2,
=2,
∴B(﹣2,0).
根据等腰梯形的对称性可得C点坐标为(4,0).
设直线AC的函数解析式为y=kx+n,
则![]() ,解得
,解得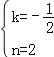 ,
,
∴直线AC的函数解析式为y=﹣![]() x+2;
x+2;
(2)设过点A,C,D的抛物线的函数解析式为y=ax2+bx+c,
则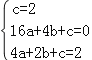 ,解得
,解得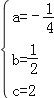 ,
,
∴y=﹣![]() x2+
x2+![]() x+2;
x+2;
(3)∵点P(m,n)(n<0)在抛物线y=﹣![]() x2+
x2+![]() x+2上,
x+2上,
∴m<﹣2或m>4,n=﹣![]() m2+
m2+![]() m+2<0,
m+2<0,
∴PM=![]() m2﹣
m2﹣![]() m﹣2.
m﹣2.
∵Rt△PCM与Rt△AOC相似,
∴![]() =
=![]() =
=![]() 或
或![]() =
=![]() =2.
=2.
①若m<﹣2,则MC=4﹣m.
当![]() =
=![]() =
=![]() 时,
时,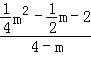 =
=![]() ,
,
解得m1=﹣4,m2=4(不合题意舍去),
此时点P的坐标为(﹣4,﹣4);
当![]() =
=![]() =2时,
=2时,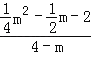 =2,
=2,
解得m1=﹣10,m2=4(不合题意舍去),
此时点P的坐标为(﹣10,﹣28);
②若m>4,则MC=m﹣4.
当![]() =
=![]() =
=![]() 时,
时,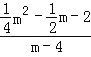 =
=![]() ,
,
解得m1=4,m2=0,均不合题意舍去;
当![]() =
=![]() =2时,
=2时,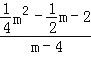 =2,
=2,
解得m1=6,m2=4(不合题意舍去),
此时点P的坐标为(6,﹣4);
综上所述,所求点P的坐标为(﹣4,﹣4)或(﹣10,﹣28)或(6,﹣4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式
① -49a2bc-14ab2c+7ab
②(2a+b)(2a-3b)-8a(2a+b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:18m2﹣32n2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
 .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为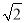 ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+ ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+ .其中正确结论的序号是( )
.其中正确结论的序号是( )
A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】填在下面各正方形中的四个数之间都有一定的规律,据此规律得出a+b+c=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次课堂练习,王莉同学做了如下4道分解因式题,你认为王莉做得不够完整的一题是( )
A. x3﹣x=x(x2﹣1) B. x2﹣2xy+y2=(x﹣y)2
C. x2y﹣xy2=xy(x﹣y) D. x2﹣y2=(x﹣y)(x+y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b,若k+b=-5,kb=6,那么该直线不经过第______________象限.
相关试题

