【题目】如图，已知八边形ABCDEFGH中4个正方形的面积分别为25，144，48，121个平方单位，PR=13（单位），则该八边形的面积= 平方单位．

参考答案：

【答案】428+66
【解析】∵4个正方形的面积分别为25，144，48，121，
∴边长分别为：5、12、4 、11，
∵PR=13、PS=12、RS=5，
∴PS⊥SR，PQ⊥QR，
∴S四边形PQRS= （PSSR+PQQR）=30+22 ，
显然S△HSG+S△CDQ=S四边形PQRS ，
如图作QI⊥PS交于I，BJ⊥AP交AP的延长线于J，
∵BP=PQ，∠BJP=∠QIP=90°，
∵∠APB+∠QPS=360°﹣90°﹣90°=180°，
∴∠QPS=∠BPJ，
∴Rt△PQI≌Rt△PBJ，
∴QI=BJ，
∴S△APB=S△PSQ ，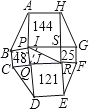
同理S△EFR=S△QSR ，
则S△APB+S△EFR=S四边形PQRS ，
故八边形的面积=3（30+22 ）+144+48+121+25，
=428+66 ．
故答案为：428+66 ．
由PR=13、PS=12、RS=5得出PS⊥SR，PQ⊥QR，求出四边形PQRS的面积，作QI⊥PS交于I，BJ⊥AP交AP的延长线于J，利用全等证出
QI=BJ，推出S△APB+S△EFR=S四边形PQRS ， 再把各部分的面积相加即可得到答案．本题主要考查了面积与等积变换，全等三角形的性质和判定，三角形的面积，勾股定理得逆定理等知识点，正确求出各部分的面积是解此题的关键．题目较好但有一定难度．

关闭