【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
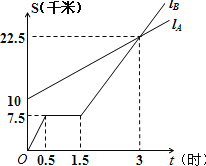
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
参考答案:
【答案】(1)10千米;(2)1小时(3)3小时(4)S=![]() t+10
t+10
【解析】
试题分析:(1)从图上可看出B出发时与A相距10千米.
(2)修理的时间就是路程不变的时间是1.5﹣0.5=1小时.
(3)从图象看出3小时时,两个图象相交,所以3小时时相遇.
(4)S和t的函数关系是一次函数,设函数是为S=kt+b,过(0,10)和(3,22.5),从而可求出关系式.
解:(1)由图形可得B出发时与A相距10千米;
(2)在图中发现0.5至1.5小时,自行车没有行走,
故可得出修理所用的时间为1小时.
(3)图中两直线的交点是B与A相遇的时刻,
即出发3小时后与A相遇.
(4)设函数是为S=kt+b,且过(0,10)和(3,22.5),
则![]() ,
,
解得:![]() .
.
故S与时间t的函数关系式为:S=![]() t+10.
t+10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体的截面一定是圆的是( )
A. 圆柱 B. 圆锥 C. 球 D. 正方体
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空,将本题补充完整.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.

解:∵EF∥AD(已知)
∴∠2= ( )
又∵∠1=∠2(已知)
∴∠1= (等量代换)
∴AB∥GD( )
∴∠BAC+ =180°( )
∵∠BAC=70°(已知)
∴∠AGD= °
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先阅读,再填空:
(x+5)(x+6)=x2+11x+30;
(x-5)(x-6)=x2-11x+30;
(x-5)(x+6)=x2+x-30;
(x+5)(x-6)=x2-x-30.
观察上面的算式,根据规律,直接写出下列各式的结果:
(a+90)(a-100)=____________; (y-80)(y-90)=____________.
(2)先阅读,再填空:
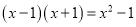 ;
;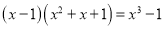 ;
; ;
;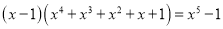 .
.观察上面各式:①由此归纳出一般性规律:
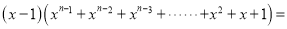 ________;
________;②根据①直接写出1+3+32+…+367+368的结果 ____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形两内角的度数之比为1:4,求这个等腰三角形顶角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把“两个邻角的角平分线互相垂直”写成“如果……,那么……”的形式为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=8131 , b=2741 , c=961 , 则a,b,c的大小关系是( )
A.a>b>c
B.a>c>b
C.a<b<c
D.b>c>a
相关试题

