【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
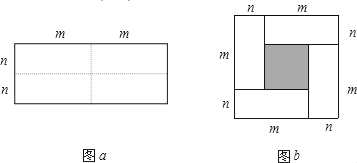
(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
参考答案:
【答案】(1)m +n; m – n;(2)(m n)2 = (m+ n)2 – 4mn,理由见解析.
【解析】
(1)观察图形很容易得出图b中大正方形的边长和阴影部分小正方形的边长;
(2)观察图形可知大正方形的面积(m+ n)2,减去阴影部分的正方形的面积(m n)2等于四块小长方形的面积4mn,即(m n)2 = (m+ n)2 – 4mn;
(1)m +n; m n
(2)解: (m n)2 = (m+ n)2 – 4mn
理由如下:右边=( m+ n)2 4 mn
=m2 + 2 mn + n2 4 mn
=m2 2 mn + n2
=(m n)2
=左边,
所以结论成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它表示甲乙两人从同一个地点出发后的情况.根据图像判断,下列说法错误的是()

A. 甲是 8 点出发的
B. 乙是 9 点出发的,到 10 点时,他大约走了 10 千米
C. 到 10 点为止,乙的速度快
D. 两人在 12 点再次相遇
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,可以得到下面的等式(1),然后将每个式子的各项系数排列成(2):(a+b)1=a+b;(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+4a3b+6a2b2+4ab3+b4;根据规律可得:(a+b)5=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m).
参考值:sin37°=0.60,cos37°=0.80,tan37°=0.75.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AO是角平分线,D为AO上一点,作△CDE,使DE=DC,∠EDC=∠BAC,连接BE.
(1)若∠BAC=60°,求证:△ACD≌△BCE;
(2)若∠BAC=90°,AD=DO,求
 的值;
的值;(3)若∠BAC=90°,F为BE中点,G为 BE延长线上一点,CF=CG,AD=nDO,直接写出
 的值.
的值.
-
科目: 来源: 题型:
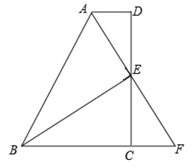
查看答案和解析>>【题目】如图,在四边形 ABCD 中,AD∥BC,E 为 CD 的中点,连接 AE、BE,延长 AE 交 BC 的 延长线于点 F.
(1)△DAE 和△CFE 全等吗?说明理由;
(2)若 AB=BC+AD,说明 BE⊥AF;
(3)在(2)的条件下,若 EF=6,CE=5,∠D=90°,你能否求出 E 到 AB 的距离?如果能 请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(13分)如图所示,四边形
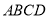 中,
中, 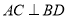 于点
于点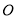 ,
, 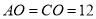 ,
, 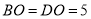 ,点
,点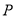 为线段
为线段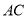 上的一个动点。
上的一个动点。(1)求证:
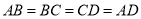 。
。(2)过点
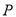 分别作
分别作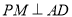 于
于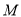 点,作
点,作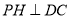 于
于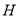 点。
点。① 试说明
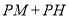 为定值。
为定值。② 连结
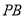 ,试探索:在点
,试探索:在点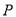 运动过程中,是否存在点
运动过程中,是否存在点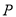 ,使
,使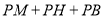 的值最小。若存在,请求出该最小值;若不存在,请说明理由。
的值最小。若存在,请求出该最小值;若不存在,请说明理由。
相关试题

