Question

【题目】边长为6的等边△ABC中，点D、E分别在AC、BC边上，DE∥AB，EC=

（1）如图1，将△DEC沿射线BC方向平移，得到△D′E′C′，边D′E′与AC的交点为M，边C′D′与∠ACC′的角平分线交于点N，当CC′多大时，四边形MCND′为菱形？并说明理由．

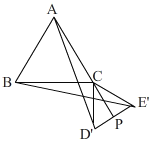
（2）如图2，将△DEC绕点C旋转∠α（0°＜α＜360°），得到△D′E′C，连接AD′、BE′．边D′E′的中点为P．

①在旋转过程中，AD′和BE′有怎样的数量关系？并说明理由；

②连接AP，当AP最大时，求AD′的值．（结果保留根号）

Answer 1

【答案】（1）；（2）①AD'=BE'，②

【解析】试题分析：（1）先判断出四边形MCND'为平行四边形，再由菱形的性质得出CN=CM，即可求出CC'；

（2）①分两种情况，利用旋转的性质，即可判断出△ACD≌△BCE'即可得出结论；②先判断出点A，C，P三点共线，先求出CP，AP，最后用勾股定理即可得出结论．

试题解析：（1）当CC'=时，四边形MCND'是菱形．

理由：由平移的性质得，CD∥C'D'，DE∥D'E'，

∵△ABC是等边三角形，∴∠B=∠ACB=60°，

∴∠ACC'=180°﹣∠ACB=120°，∵CN是∠ACC'的角平分线，

∴∠D'E'C'=∠ACC'=60°=∠B，

∴∠D'E'C'=∠NCC'，∴D'E'∥CN，

∴四边形MCND'是平行四边形，

∵∠ME'C'=∠MCE'=60°，∠NCC'=∠NC'C=60°，

∴△MCE'和△NCC'是等边三角形，

∴MC=CE'，NC=CC'，

∵E'C'=2，

∵四边形MCND'是菱形，

∴CN=CM，

∴CC'=E'C'=；

（2）①AD'=BE'，

理由：当α≠180°时，由旋转的性质得，∠ACD'=∠BCE'，

由（1）知，AC=BC，CD'=CE'，∴△ACD'≌△BCE'，∴AD'=BE'，

当α=180°时，AD'=AC+CD'，BE'=BC+CE'，即：AD'=BE'，

综上可知：AD'=BE'．

②如图连接CP，

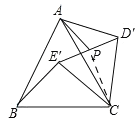
在△ACP中，由三角形三边关系得，AP＜AC+CP，

∴当点A，C，P三点共线时，AP最大，

如图所示，

在△D'CE'中，由P为D'E的中点，得AP⊥D'E'，PD'=，

∴CP=3，∴AP=6+3=9，

在Rt△APD'中，由勾股定理得，AD'=．