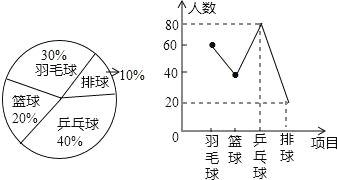
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面调查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题.

(1)在这次调查活动中,一共调查了 名学生,并请补全统计图.
(2)“羽毛球”所在的扇形的圆心角是 度.
(3)若该校有学生1200名,估计爱好乒乓球运动的约有多少名学生?
参考答案:
【答案】(1)200,补图见解析;(2)108;(3)480.
【解析】
试题分析:(1)读图可知喜欢乒乓球的有80人,占40%.所以一共调查了80÷40%=200人;
(2)喜欢排球的20人,应占![]() ×100%=10%,喜欢羽毛球的应占统计图的1-20%-40%-10%=30%,所占的圆心角为360°×30%=108°;
×100%=10%,喜欢羽毛球的应占统计图的1-20%-40%-10%=30%,所占的圆心角为360°×30%=108°;
(3)利用样本估计总体的办法,计算出答案即可.
试题解析:(1)80÷40%=200(人)
喜欢篮球的人数:200×20%=40(人),
喜欢羽毛球的人数:200-80-20-40=60(人),
如图所示:
(2)![]() ×100%=10%,
×100%=10%,
1-20%-40%-10%=30%,
360°×30%=108°;
(3)喜欢乒乓球的人数:40%×1200=480(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC,DE=EF,AE=EC,则图中的四边形ADCF是__,四边形BCFD是__.(选填“平行四边形、矩形、菱形、正方形”)

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣0.125×18
 ×8
×8(2)﹣24×(
 ﹣
﹣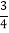 +
+ )
)(3)91
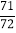 ×(﹣36)
×(﹣36)(4)﹣4×(﹣8
 )+(﹣8)×(﹣8
)+(﹣8)×(﹣8 )+12×(﹣8
)+12×(﹣8 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=
 x2﹣3x+4,
x2﹣3x+4,
(1)配方成y=a(x﹣h)2+k的形式.
(2)求出它的图象的顶点坐标和对称轴.
(3)求出函数的最大或最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,不正确的是( )
A. 平方等于本身的数只有
 和
和 B. 正数的绝对值是它本身,负数的绝对值是它的相反数
B. 正数的绝对值是它本身,负数的绝对值是它的相反数C. 两个数的差为正数,至少其中有一个正数 D. 两个负数,绝对值大的负数反而小
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将周长为10的△ABC沿BC方向平移l个单位,得到△DEF,则四边形ABFD的周长是( )

A.12
B.14
C.15
D.16
相关试题

