【题目】已知在数轴上有A,B两点,点A表示的数为4,点B在A点的左边,且AB=12.若有一动点P从数轴上点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿着数轴向右匀速运动,设运动时间为t秒.
![]()
(1)写出数轴上点B表示的数为________,P所表示的数为________(用含t的代数式表示);
(2)若点P,Q分别从A,B两点同时出发,问点P运动多少秒与Q相距3个单位长度?
(3)若点P,Q分别从A,B两点同时出发,分别以BQ和AP为边,在数轴上方作正方形BQCD和正方形APEF如图所示.求当t为何值时,两个正方形的重叠部分面积是正方形APEF面积的一半?请直接写出结论:t=__________秒.

参考答案:
【答案】(1)-8,4-t;(2)3或5;(3)4.8或24.
【解析】
(1)根据已知可得B点表示的数为4-12;点P表示的数为4-t;
(2) 设点P运动x秒时,与Q相距3个单位长度,分两种情况:P点在Q点右侧,P点在Q点左侧,分别列出方程即可求解;
(3)可分两种情况:如图一,P、Q在线段AB上;如图二、P、Q在线段AB外,根据题意列出关于t的方程即可求解.
(1)∵点A表示的数为4,B在A点左边,AB=12,
∴点B表示的数是412=8,
∵动点P从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,
∴点P表示的数是4t.
(2)设点P运动x秒时,与Q相距3个单位长度,分两种情况:
![]()
P点在Q点右侧时:
则AP=x,BQ=2x,
∵AP+BQ=AB3,
∴x+2x=9,
解得:x=3,
![]()
P点在Q点左侧时:
∵AP+BQ=AB+3,
∴x+2x=15
解得:x=5.
∴点P运动3秒或5秒时与点Q相距3个单位长度。
(3) 分两种情况:
如图一: 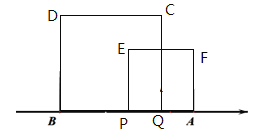
图一
∵两个正方形的重叠部分面积是正方形APEF面积的一半,AP=t,BQ=2t,
∴AQ=PQ=![]() ,
,
∴2t+![]() =12 解得t=4.8
=12 解得t=4.8
如图二: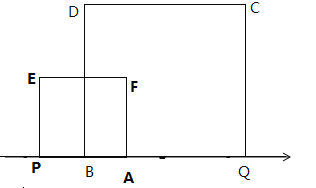
图二
∵两个正方形的重叠部分面积是正方形APEF面积的一半,AP=t,BQ=2t,
∴AB=PB=![]() ,
,
∴![]() =12 解得t=24.
=12 解得t=24.
故答案为:(1)-8,4-t;(2)3或5;(3)4.8或24.
-
科目: 来源: 题型:
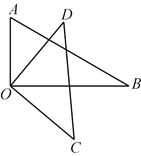
查看答案和解析>>【题目】如图,将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)判断大小关系:∠AOD______∠BOC(填>、=、<等)
(2)若 ∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= ;
(3)猜想 ∠AOC与∠BOD的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动______ 秒时,△DEB与△BCA全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2tan60°﹣|
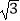 ﹣2|﹣
﹣2|﹣ 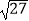 +(
+(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
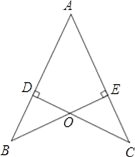
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
-
科目: 来源: 题型:
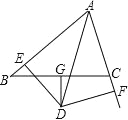
查看答案和解析>>【题目】如图,G 为 BC 的中点,且 DG⊥BC,DE⊥AB 于 E,DF⊥AC 于 F, BE=CF.
(1)求证:AD 是∠BAC 的平分线;
(2)如果 AB=8,AC=6,求 AE 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.

解:∵∠1+∠2=180°(已知),
∠1+∠EFD=180°(邻补角定义),
∴∠2=∠EFD( )
∴AB∥EF(内错角相等,两直线平行)
∴∠ADE=∠3( )
∵∠3=∠B(已知)
∴∠ADE=∠B( )
∴ (同位角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等).
相关试题

