【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.

(1)求证:AD⊥CD;(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
参考答案:
【答案】(1)、证明过程见解析;(2)、2.5
【解析】
试题分析:(1)、连接OC,根据OA=OC得出∠OAC=∠OCA,根据AC平分∠DAB得到∠OAC=∠DAC,从而说明∠OCA=∠DAC,得到AD∥OC,从而说明切线;(2)、连接CB,根据AB为直径得到∠ACB=90°,根据已知条件得到∠ADC=90°,结合∠DAC=∠CAB得到△DAC∽△CAB,从而得出AB的长度.
试题解析:(1)、连接OC
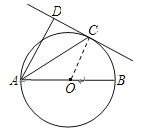
∵OA=OC ∴∠OAC=∠OCA
∵AC平分∠DAB ∴∠OAC=∠DAC ∴∠OCA=∠DAC ∴AD∥OC
∵直线CD与⊙O相切 ∴OC⊥CD ∴AD⊥CD
(2)、连接CB
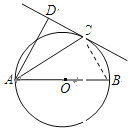
∵AB是⊙O直径 ∴∠ACB=90°
由(1)知AD⊥CD ∴∠ADC=90°∴∠ADC=∠ACB ∵∠DAC=∠CAB ∴△DAC∽△CAB
∴![]() 即
即![]() ∴AB=2.5
∴AB=2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.

(1)求证:BC平分∠ABE;(2)若∠ABC=30°,OA=4,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若
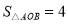 .
.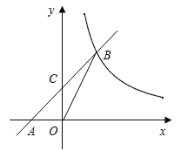
(1)求该反比例函数的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,且
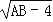 +|BC﹣6|=0,点P、Q分别是边AD、AB上的动点.
+|BC﹣6|=0,点P、Q分别是边AD、AB上的动点.(1)求BD的长(长度单位是cm);
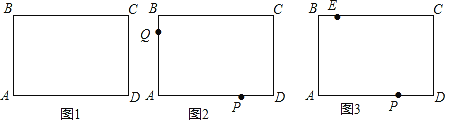
(2)如图2,若点P从D点出发,以2cm/s的速度沿DA向点A运动,点Q从B点出发,以1cm/s的速度沿BA向点A运动,P、Q同时出发,一个点到达终点时,两点同时停止运动;设运动时间为x,用含x的代数式表示△CPQ的面积S.
(3)如图3,在BC上取一点E,使EB=1,那么当△EPC是等腰三角形时,请直接写出△EPC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产的某种产品按质量分为10个等级.第1级(最低级)产品每天能生产95件,每件利润6元.已知每提高一个级别,每件利润增加2元,但每天产量减少5件.
(1)若生产第3级产品,则每天产量为 件,每件利润为 元;
(2)若生产第x级产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数解析式;
(3)若生产第x级的产品一天的总利润为1120元,求该产品的质量等级.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校艺术节文艺汇演中,甲、乙两个舞蹈队队员的身高的方差依次是1.5、2.5,那么身高更整齐的是_________队(填"甲"或"乙"),
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=-2x2的开口方向是______,它的形状与y=2x2的形状______,它的顶点坐标是______,对称轴是______.
相关试题

