【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.

(1)求证:BC平分∠ABE;(2)若∠ABC=30°,OA=4,求CE的长.
参考答案:
【答案】(1)、证明过程见解析;(2)、2![]()
【解析】
试题分析:(1)、连接OC,根据相切可得OC⊥CD,结合BE⊥CD得出OC∥BE,则∠OCB=∠EBC,根据OC=∠OB得出∠OCB=∠OBC,即∠EBC=∠OBC,从而得到角平分线;(2)、过A做CF⊥AB于F,根据AB为直角可得∠ACB=90°,根据∠ABC的度数得出∠A的度数,从而得出AC=4,根据Rt△ACF的三角形函数得出CF的长度,根据角平分线的性质得出CE=CF.
试题解析:(1)、连接OC ∵CD切⊙O于C ∴OC⊥CD ∵BE⊥CD ∴OC∥BE
∴∠OCB=∠EBC ∵OC=∠OB ∴∠OCB=∠OBC ∴∠EBC=∠OBC ∴BC平分∠ABE
(2)、过A做CF⊥AB于F ∵AB是⊙O的直径 ∴∠ACB=90° ∵∠ABC=30°∴∠A=60°
∴![]() 在Rt△ACF中,∠A=60°, ∴
在Rt△ACF中,∠A=60°, ∴![]()
∴![]() ∵BC平分∠ABE,CF⊥AB,∵CE⊥BE ∴
∵BC平分∠ABE,CF⊥AB,∵CE⊥BE ∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x 2 +x=2,则下列说中,正确的是( )
A. 方程两根之和是1 B. 方程两根之和是-1
C. 方程两根之积是2 D. 方程两根之差是-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果正多边形的一个外角为72°,那么它的边数是_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华用两块不全等的等腰直角三角形的三角板摆放图形.

(1)如图①所示两个等腰直角△ABC,△DBE,两直角边交于点F,连接BF、AD,求证:BF=AD;
(2)如果小华将两块三角板△ABC,△DBE如图②所示摆放,使D、B、C三点在一条直线上,AC、DE的延长线相交于点F,过点F作FG∥BC,交直线AE于点G,连接AD,FB,求证:FG=AC+DC;
(3)在(2)的条件下,若AG=7
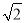 ,DC=5,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段FG于P、Q两点(如图③),若PG=2,求线段FQ的长.
,DC=5,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段FG于P、Q两点(如图③),若PG=2,求线段FQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若
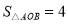 .
.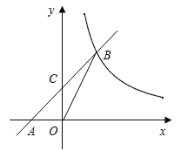
(1)求该反比例函数的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
-
科目: 来源: 题型:
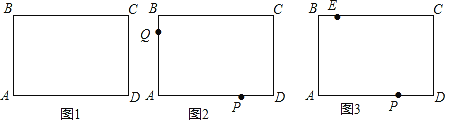
查看答案和解析>>【题目】如图1,长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,且
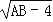 +|BC﹣6|=0,点P、Q分别是边AD、AB上的动点.
+|BC﹣6|=0,点P、Q分别是边AD、AB上的动点.(1)求BD的长(长度单位是cm);
(2)如图2,若点P从D点出发,以2cm/s的速度沿DA向点A运动,点Q从B点出发,以1cm/s的速度沿BA向点A运动,P、Q同时出发,一个点到达终点时,两点同时停止运动;设运动时间为x,用含x的代数式表示△CPQ的面积S.
(3)如图3,在BC上取一点E,使EB=1,那么当△EPC是等腰三角形时,请直接写出△EPC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.

(1)求证:AD⊥CD;(2)若AD=2,AC=
 ,求AB的长.
,求AB的长.
相关试题

