【题目】某商品现在售价为每件40元,每天可卖200件,该商品将从现在起进行90天的销售:在第x(1≤x≤49)天内,当天售价都较前一天增加1元,销量都较前一天减少2件;在x(50≤x≤90)天内,当天的售价都是90元,销售仍然是较前一天减少2件,已知该商品的进价为每件30元,设销售商品的当天利润为y元.
(1)求出y与x的函数关系式;
(2)销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天当天销售利润不低于4800元?
参考答案:
【答案】(1)y=![]() ;(2)销售该商品第45天时,销售利润最大,最大利润为6050元.(3)共有41天当天销售利润不低于4800元.
;(2)销售该商品第45天时,销售利润最大,最大利润为6050元.(3)共有41天当天销售利润不低于4800元.
【解析】
(1)根据:总利润=(售价﹣成本)×销售量,结合x的取值范围可列函数关系式;
(2)根据分段函数的性质,可分别得出最大值,比较大小可得答案;
(3)根据二次函数值大于或等于4800,一次函数值大于或等于48000,可得不等式,解不等式即可的x的范围,可得答案
(1)当1≤x≤49时,当天售价为(40+x)元,出售商品(200﹣2x)件,∴y=(40+x﹣30)(200﹣2x)=﹣2x2+180x+2000;
当50≤x≤90时,当天售价为90元,出售量为(200﹣2x),∴y=(90﹣30)(200﹣2x)=﹣120x+12000;
∴y=![]() .
.
(2)当1≤x≤49时,y=﹣2x2+180x+2000=﹣2(x﹣45)2+6050,∴当x=45时,y取得最大值6050;
当50≤x≤90时,由y=﹣120x+12000知,y随x的增大而减小,∴当x=50时,y取得最大值6000.
∵6050>6000,∴销售该商品第45天时,销售利润最大,最大利润为6050元.
(3)①当1≤x≤49时,﹣2x2+180x+2000≥4800,
解得:20≤x≤70,∴20≤x≤49;
②当50≤x≤90时,﹣120x+12000≥4800,
解得:x≤60,∴50≤x≤60;
综上:20≤x≤60,∴从第20天起直到第60天止,每天的销售利润都不低于4800元,
故共有41天当天销售利润不低于4800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,若分得的两个小三角形中一个三角形为等腰三角形,另一个三角形的三个内角与原来三角形的三个内角分别相等,则称这条线段叫做这个三角形的“等角分割线”.
例如,等腰直角三角形斜边上的高就是这个等腰直角三角形的一条“等角分割线”.

(1)如图1,在△ABC中,D是边BC上一点,若∠B=30°,∠BAD=∠C=40°,求证: AD为△ABC的“等角分割线”;
(2)如图2,△ABC中,∠C=90°,∠B=30°;
①画出△ABC的“等角分割线”,写出画法并说明理由;
②若BC=3,求出①中画出的“等角分割线”的长度.
(3)在△ABC中,∠A=24°,若△ABC存在“等角分割线”CD,直接写出所有符合要求的∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是常见的安全标记,其中是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线l:y=
 x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y= x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,若AC=6,则DE的长为( )
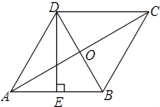
A. 3 B. 3
 C. 2
C. 2 D. 4
D. 4
相关试题

