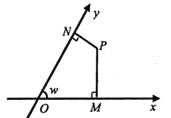
【题目】定义:在同一平面内画两条相交、有公共原点的数轴x轴和y轴,交角a≠90°,这样就在平面上建立了一个斜角坐标系,其中w叫做坐标角,对于坐标平面内任意一点P,过P作y轴和x轴的平行线,与x轴、y轴相交的点的坐标分别是a和b,则称点P的斜角坐标为(a,b).如图,w=60°,点P的斜角坐标是(1,2),过点P作x轴和y轴的垂线,垂足分别为M、N,则四边形OMPN的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
参考答案:
【答案】B
【解析】
添加辅助线,将四边形OMPN转化为直角三角形和平行四边形,因此过点P作PA∥y轴,交x轴于点A,过点P作PB∥x轴交y轴于点B,易证四边形OAPB是平行四边形,利用平行四边形的性质,可知OB=PA,OA=PB,由点P的斜角坐标就可求出PB、PA的长,再利用解直角三角形分别求出PN,NB,PM,AM的长,然后根据S四边形OMPN=S△PAM+S△PBN+S平行四边形OAPB , 利用三角形的面积公式和平行四边形的面积公式,就可求出结果.
解:过点P作PA∥y轴,交x轴于点A,过点P作PB∥x轴交y轴于点B,
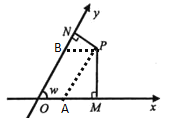
∴四边形OAPB是平行四边形,∠NBP=w=∠PAM=60°,
∴OB=PA,OA=PB
∵点P的斜角坐标为(1,2),
∴OA=1,OB=2,
∴PB=1,PA=2,
∵PM⊥x轴,PN⊥y轴,
∴∠PMA=∠PNB=90°,
在Rt△PAM中,∠PAM=60°,则∠APM=30°,
∴PA=2AM=2,即AM=1
PM=PAsin60°
∴PM=![]()
∴S△PAM=![]()
在Rt△PBN中,∠PBN=60°,则∠BPN=30°,
∴PB=2BN=1,即BN=![]()
PN=PBsin60°
∴PN=![]()
∴S△PBN=![]() ,
,
∵S四边形OMPN=S△PAM+S△PBN+S平行四边形OAPB
![]()
故答案为:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
2016年,北京市坚持创新、协调、绿色、开放、共享的发展理念,围绕首都城市战略定位,加快建设国际一流的和谐宜居之都,在教育、科技等方面保持平稳健康发展,实现了“十三五”良好开局.
在教育方面,全市共有58所普通高校和81个科研机构培养研究生,全年研究生招生9.7万人,在校研究生29.2万人.全市91所普通高校全年招收本专科学生15.5万人,在校生58.8万人.全市成人本专科招生6.1万人,在校生17.2万人.
在科技方面,2016年全年研究与试验发展(R&D)经费支出1479.8亿元,比2015年增长了6.9%,全市研究与试验发展(R&D)活动人员36.2万人,比上年增长1.1万人.2013年,2014年,2015年全年研究与试验发展(R&D)经费支出分别为1185.0亿元,1268.8亿元,1384.0亿元,分别比前一年度增长11.4%,7.1%,9.1%.
(以上数据来源于北京市统计局)
根据以上材料解答下列问题:
(1)请用统计图或统计表将北京市2016年研究生、普通高校本专科学生、成人本专科学生的招生人数和在校生人数表示出来;
(2)2015年北京市研究与试验发展(R&D)活动人员为 万人;
(3)根据材料中的信息,预估2017年北京市全年研究与试验发展(R&D)经费支出约 亿元,你的预估理由是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,货轮甲从港口O出发,沿东偏南
 的方向航行20海里后到达A处.(已知四个圆圈的半径(由小到大)分别是5海里,10海里,15海里,20海里.)
的方向航行20海里后到达A处.(已知四个圆圈的半径(由小到大)分别是5海里,10海里,15海里,20海里.)
(1)写出在港口O观测灯塔B,C的方向及它们与港口的距离;
(2)已知灯塔D在港口O的南偏西
 方向上,且与灯塔B相距35海里,在图中标出灯塔D的位置.
方向上,且与灯塔B相距35海里,在图中标出灯塔D的位置.(3)货轮乙从港口O出发,沿正东方向航行15海里到达P处后,需把航行方向调整到与货轮甲的航行方向一致,此时货轮乙应向左(或右)转多少度?并画出货轮乙航行线路示意图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】佳佳想探究一元三次方程x3+2x2-x-2=0的解的情况.根据以往的学习经验他想到了方程与函数的关系:一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一次方程kx+b=0(k≠0)的解;二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解.如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为方程x2-2x-3=0的解.
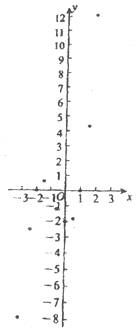
根据以上方程与函数的关系,若知道函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知道方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象:

(1)直接写出m的值________,并画出函数图象;
(2)根据表格和图象可知,方程的解有________个,分别为________________;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为( )

A.
 B.
B.  C. 3 D. 5
C. 3 D. 5
相关试题

