【题目】小明和小亮两人从甲地出发,沿相同的线路跑向乙地,小明先跑一段路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,两人一起以小明原来的速度跑向乙地,如图是小明、小亮两人在跑步的全过程中经过的路程y(米)与小明出发的时间x(秒)的函数图象,请根据题意解答下列问题:
(1)在跑步的全过程中,小明共跑了 米,小明的速度为 米/秒.
(2)求小亮跑步的速度及小亮在途中等候小明的时间;
(3)求小亮出发多长时间第一次与小明相遇?
参考答案:
【答案】(1)900,1.5;(2)小亮跑步的速度是2.5米/秒,小亮在途中等候小明的时间是100秒;(3)小亮出发150秒时第一次与小明相遇.
【解析】
(1)观察图象可知小明共跑了900米,用了600秒,根据路程÷时间=速度,即可求出小明的速度;
(2)根据图象先求出小亮超过小明150米时,小明所用的时间,然后据此求出小亮的速度,小明赶上小亮时所用的时间-小亮在等候小明前所用的时间=小亮在途中等候小明的时间,据此计算即可;
(3)设小亮出发t秒时第一次与小明相遇,根据(1)、(2)计算出的小亮和小明的速度列出方程求解即可.
解:(1)由图象可得,
在跑步的全过程中,小明共跑了900米,小明的速度为:900÷600=1.5米/秒,
故答案为:900,1.5;
(2)当x=500时,y=1.5×500=750,
当小亮超过小明150米时,小明跑的路程为:750﹣150=600(米),此时小明用的时间为:600÷1.5=400(秒),
故小亮的速度为:750÷(400﹣100)=2.5米/秒,
小亮在途中等候小明的时间是:500﹣400=100(秒),
即小亮跑步的速度是2.5米/秒,小亮在途中等候小明的时间是100秒;
(3)设小亮出发t秒时第一次与小明相遇,
2.5t=1.5(t+100),
解得,t=150,
答:小亮出发150秒时第一次与小明相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:M=3a2+4ab -5a-6,N=a2-2ab-4
(1)化简:5M-(3N + 4M),结果用含a、b的式子表示.
(2)若式子5M-(3N + 4M)的值与字母a的取值无关,求b4+
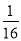 M-
M-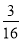 N-
N- 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(
 ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
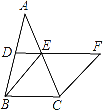
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
-
科目: 来源: 题型:
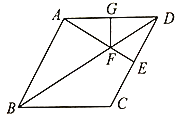
查看答案和解析>>【题目】如图,在菱形
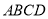 中,
中,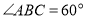 ,过点
,过点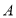 作
作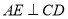 于点
于点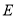 ,交对角线
,交对角线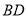 于点
于点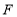 ,过点
,过点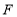 作
作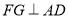 于点
于点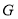 .
.
(1)若
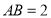 ,求四边形
,求四边形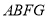 的面积;(2)求证:
的面积;(2)求证: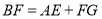 .(温馨提示;连接
.(温馨提示;连接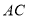 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:多项式式x2-2xy-1的常数项是a,次数是b.
(1)计算:a2-2ab + b2-10的值.
(2)点A在数轴上表示的有理数是a,点B在数轴上表示的有理数是b,数轴上A、B之间的距离记作
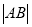 定义:
定义: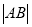 =
=
①设点P在数轴上对应的数为t,当
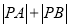 =13时,求:t2-5t +7的值.
=13时,求:t2-5t +7的值.②式子
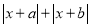 的最小值是________,取得最小值时x的取值范围是_____.
的最小值是________,取得最小值时x的取值范围是_____.
相关试题

