【题目】如图,在菱形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交对角线
,交对角线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
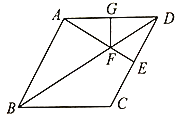
(1)若![]() ,求四边形
,求四边形![]() 的面积;(2)求证:
的面积;(2)求证:![]() .(温馨提示;连接
.(温馨提示;连接![]() )
)
参考答案:
【答案】(1)四边形![]() 的面积是
的面积是![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)首先求出△ABD的面积,再求出RT△DFG的面积是,进而可求出四边形ABFG的面积是.
(2) 连结AC,交BD于点O,根据已知条件和菱形的性质看证明△ABO≌△DAE和△AOF≌△AGF,由全等三角形的性质即可证明BF=AE+FG
(1)∵∠1=∠2=30,
∴AF=DF.
又∵FG⊥AD于点G,
∴AG=![]() AD,
AD,
∵AB=2,
∴AD=2,AG=1.
∴DG=1,AO=1,FG=![]() ,BD=
,BD=![]() ,
,
∴△ABD的面积是![]() ,RT△DFG的面积是
,RT△DFG的面积是![]()
∴四边形ABFG的面积是53√6.∴四边形![]() 的面积是
的面积是![]() .
.
(2)证明:连结![]() 交
交![]() 于点
于点![]() .
.
∵四边形ABCD是菱形,
∴AB=AD,∠ABC=∠ADC,∠4=12∠ABC,∠2=12∠ADC,AC⊥BD,
∵∠ABC=60,
∴∠2=∠4=12∠ABC=30,
又∵AE⊥CD于点E,
∴∠AED=90,
∴∠1=30,
∴∠1=∠4,∠AOB=∠DEA=90,
∴△ABO≌△DAE,
∴AE=BO.
又∵FG⊥AD于点G,
∴∠AOF=∠AGF=90,
又∵∠1=∠3,AF=AF,
∴△AOF≌△AGF,
∴FG=FO.
∴BF=AE+FG.
-
科目: 来源: 题型:
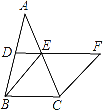
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮两人从甲地出发,沿相同的线路跑向乙地,小明先跑一段路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,两人一起以小明原来的速度跑向乙地,如图是小明、小亮两人在跑步的全过程中经过的路程y(米)与小明出发的时间x(秒)的函数图象,请根据题意解答下列问题:
(1)在跑步的全过程中,小明共跑了 米,小明的速度为 米/秒.
(2)求小亮跑步的速度及小亮在途中等候小明的时间;
(3)求小亮出发多长时间第一次与小明相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:多项式式x2-2xy-1的常数项是a,次数是b.
(1)计算:a2-2ab + b2-10的值.
(2)点A在数轴上表示的有理数是a,点B在数轴上表示的有理数是b,数轴上A、B之间的距离记作
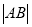 定义:
定义: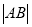 =
=
①设点P在数轴上对应的数为t,当
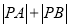 =13时,求:t2-5t +7的值.
=13时,求:t2-5t +7的值.②式子
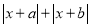 的最小值是________,取得最小值时x的取值范围是_____.
的最小值是________,取得最小值时x的取值范围是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台)
售价(元/台)
电饭煲
200
250
电压锅
160
200
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的
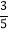 ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点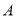 在
在 轴上,点
轴上,点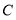 在
在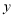 轴上,
轴上, ,
, ,过点
,过点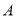 的直线交矩形
的直线交矩形 的边
的边 于点
于点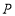 ,且点
,且点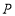 不与点
不与点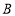 、
、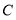 重合,过点
重合,过点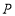 作
作 ,
,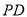 交
交 轴于点
轴于点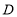 ,交
,交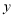 轴于点
轴于点 .
.(1)如图1,若
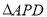 为等腰直角三角形,求直线
为等腰直角三角形,求直线 的函数解析式;
的函数解析式;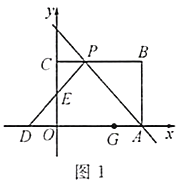
(2)如图2,过点
 作
作 交
交 轴于点
轴于点 ,若四边形
,若四边形 是平行四边形,求直线
是平行四边形,求直线 的解析式.
的解析式.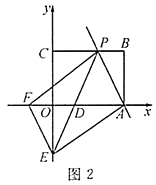
相关试题

