【题目】将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB= ![]() ,P是AC上的一个动点.
,P是AC上的一个动点. 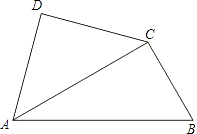
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
参考答案:
【答案】
(1)解:在Rt△ABC中,AB=2 ![]() ,∠BAC=30°,
,∠BAC=30°,
∴BC= ![]() ,AC=3.
,AC=3.
如图(1),作DF⊥AC.
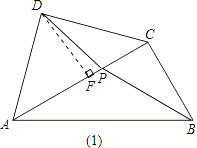
∵Rt△ACD中,AD=CD,
∴DF=AF=CF= ![]() .
.
∵BP平分∠ABC,
∴∠PBC=30°,
∴CP=BCtan30°=1,
∴PF= ![]() ,
,
∴DP= ![]() =
= ![]()
(2)解:当P点位置如图(2)所示时,
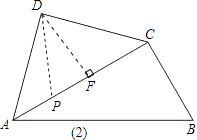
根据(1)中结论,DF= ![]() ,∠ADF=45°,
,∠ADF=45°,
又∵PD=BC= ![]() ,
,
∴cos∠PDF= ![]() =
= ![]() ,
,
∴∠PDF=30°.
∴∠PDA=∠ADF﹣∠PDF=15°.
当P点位置如图(3)所示时,
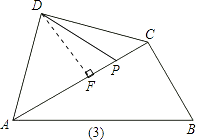
同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.
故∠PDA的度数为15°或75°;
(3)解:当点P运动到边AC中点(如图4),即CP= ![]() 时,
时,
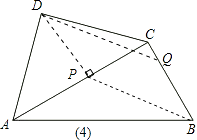
以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上.
∵四边形DPBQ为平行四边形,
∴BC∥DP,
∵∠ACB=90°,
∴∠DPC=90°,即DP⊥AC.
而在Rt△ABC中,AB=2 ![]() ,BC=
,BC= ![]() ,
,
∴根据勾股定理得:AC=3,
∵△DAC为等腰直角三角形,
∴DP=CP= ![]() AC=
AC= ![]() ,
,
∵BC∥DP,
∴PC是平行四边形DPBQ的高,
∴S平行四边形DPBQ=DPCP= ![]() .
.
【解析】(1)作DF⊥AC,由AB的长求得BC、AC的长.在等腰Rt△DAC中,DF=FA=FC;在Rt△BCP中,求得PC的长.则由勾股定理即可求得DP的长.(2)由(1)得BC与DF的关系,则DP与DF的关系也已知,先求得∠PDF的度数,则∠PDA的度数也可求出,需注意有两种情况.(3)由于四边形DPBQ为平行四边形,则BC∥DF,P为AC中点,作出平行四边形,求得面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
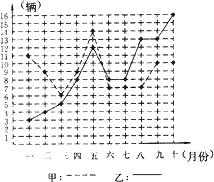
(1)请你根据上图填写下表:销售公司
平均数
方差
中位数
众数
甲
5.2
9
乙
9
17.0
8
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: ①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力). -
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形、等边三角形、正方形、直角三角形这四类图形中,既是轴对称图形,又是中心对称图形的是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
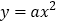 的图象与一次函数
的图象与一次函数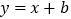 的图象相交于
的图象相交于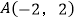 、
、 两点,从点
两点,从点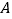 和点
和点 分别引平行于
分别引平行于 轴的直线与
轴的直线与 轴分别交于
轴分别交于 ,
, 两点,点
两点,点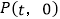 为线段
为线段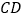 上的动点,过点
上的动点,过点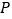 且平行于
且平行于 轴的直线与抛物线和直线分别交于
轴的直线与抛物线和直线分别交于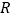 ,
,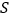 .
.(1)求一次函数和二次函数的解析式,并求出点
 的坐标.
的坐标.(2)当SR=2RP时,计算线段SR的长.
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使
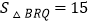 .若存在,求
.若存在,求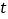 的值;若不存在,说明理由.
的值;若不存在,说明理由.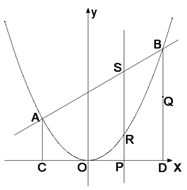
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班数学兴趣小组8名同学的毕业升学体育测试成绩依次为:30,29,28,27,28,29,30,28,这组数据的众数是( )
A. 27 B. 28 C. 29 D. 30
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
-
科目: 来源: 题型:
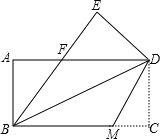
查看答案和解析>>【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
相关试题

