【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: 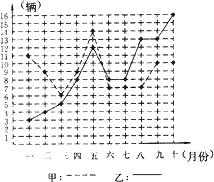
(1)请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 5.2 | 9 | ||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: ①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).
参考答案:
【答案】
(1)解:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 9 | 5.2 | 9 | 7 |
乙 | 9 | 17.0 | 8 | 8 |
(2)解:①∵甲、乙的平均数相同,而S2甲<S2乙,
∴甲汽车销售公司比乙汽车销售公司的销售情况较稳定;
②因为甲汽车销售公司每月销售的数量在平均数上下波动,而乙汽车销售公司每月销售的数量处于上升势头,从六月份起都比甲汽车销售公司销售数量多,所以乙汽车销售公司的销售有潜力
【解析】(1)根据平均数、方差、中位数的概念求值,并填表;(2)根据方差分析稳定性,根据销售趋势看销售前景即可求出答案.
【考点精析】根据题目的已知条件,利用折线统计图和算术平均数的相关知识可以得到问题的答案,需要掌握能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比;总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣
 )2=0.
)2=0.(2)先化简,再求值:﹣(3x2﹣4xy)﹣
 [x2﹣2(4x﹣4xy)],其中x=﹣2.
[x2﹣2(4x﹣4xy)],其中x=﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是( )
A.20cm2
B.20πcm2
C.10πcm2
D.5πcm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选一个,并选择你认为适当的方法解这个方程.
①x2﹣4x﹣1=0
②x(2x+1)=8x﹣3
③x2+3x+1=0
④x2﹣9=4(x﹣3)
我选择第个方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形、等边三角形、正方形、直角三角形这四类图形中,既是轴对称图形,又是中心对称图形的是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
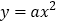 的图象与一次函数
的图象与一次函数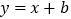 的图象相交于
的图象相交于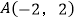 、
、 两点,从点
两点,从点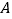 和点
和点 分别引平行于
分别引平行于 轴的直线与
轴的直线与 轴分别交于
轴分别交于 ,
, 两点,点
两点,点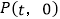 为线段
为线段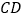 上的动点,过点
上的动点,过点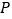 且平行于
且平行于 轴的直线与抛物线和直线分别交于
轴的直线与抛物线和直线分别交于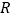 ,
,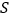 .
.(1)求一次函数和二次函数的解析式,并求出点
 的坐标.
的坐标.(2)当SR=2RP时,计算线段SR的长.
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使
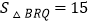 .若存在,求
.若存在,求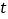 的值;若不存在,说明理由.
的值;若不存在,说明理由.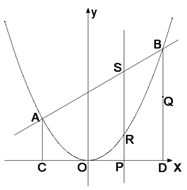
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=
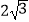 ,P是AC上的一个动点.
,P是AC上的一个动点. 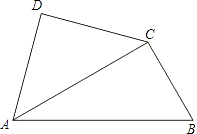
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
相关试题

