【题目】如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要个小立方块.最终搭成的长方体的表面积是 . 
参考答案:
【答案】26;66
【解析】解:由俯视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1个小立方体,
其小正方块分布情况如下:
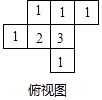
那么共有7+2+1=10个几何体组成.
若搭成一个大长方体,共需3×4×3=36个小立方体,
所以还需36﹣10=26个小立方体,
最终搭成的长方体的表面积是3×4×2+3×3×2+3×4×2=66
所以答案是:26,66.
【考点精析】本题主要考查了由三视图判断几何体的相关知识点,需要掌握在三视图中,通过主视图、俯视图可以确定组合图形的列数;通过俯视图、左视图可以确定组合图形的行数;通过主视图、左视图可以确定行与列中的最高层数才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若 =
=  ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH . 
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】任选一题作答,只计一题的成绩:
a.如图,在
 的正方形网格中,点
的正方形网格中,点 ,
, ,
, ,
, ,
, ,
, 都在格点上.连接点
都在格点上.连接点 ,
, 得线段
得线段 .
.
(1)画出过
 ,
, ,
, ,
, 中的任意两点的直线;
中的任意两点的直线;(2)互相平行的直线(线段)有 ;(请用“
 ”表示)
”表示)(3)互相垂直的直线(线段)有 .
(请用“
 ”表示)
”表示)b.如图,直线
 和
和 相交于
相交于 ,
, ,
, 是
是 的角平分线,
的角平分线, ,求
,求 的度数.
的度数.其中一种解题过程如下,请在括号中注明根据,在横线上补全步骤.
解:






 是
是 的角平分线
的角平分线















-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题化简及计算
(1)化简: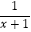 ﹣
﹣ 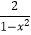
(2)关于x的一元二次方程kx2﹣2x+3=0有两个不相等的实数根.求:k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
组别
成绩x(分)
频数(人数)
频率
一
50≤x<60
2
0.04
二
60≤x<70
10
0.2
三
70≤x<80
14
b
四
80≤x<90
a
0.32
五
90≤x<100
8
0.16
请根据表格提供的信息,解答以下问题:

(1)直接写出表中a= , b=;
(2)请补全右面相应的频数分布直方图;
(3)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .
(4)请根据得到的统计数据,简要分析这些同学的汉字书写能力,并为提高同学们的书写汉字能力提一条建议(所提建议不超过20字) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上, 点A的坐标为(2,4).
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A的对应点坐标A1 .
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标A2 .
(3)设BC边上的高AD,则AD= .

相关试题

