【题目】已知如图,![]() 三点在同一直线上,
三点在同一直线上,![]() .
.
(1)已知点![]() 在直线
在直线![]() 上,根据条件,请补充完整图形,并求
上,根据条件,请补充完整图形,并求![]() 的长;
的长;
![]()
(2)已知点![]() 在直线
在直线![]() 上,
上,![]() 分别是
分别是![]() ,
,![]() 的中点,根据条件,请补充完整图形,并求
的中点,根据条件,请补充完整图形,并求![]() 的长,直接写出
的长,直接写出![]() 与
与![]() 的长存在的数量关系;
的长存在的数量关系;
![]()
(3)已知点![]() 在直线
在直线![]() 上,
上,![]() 分别是
分别是![]() ,
,![]() 的中点,根据条件,请补充完整图形,并求
的中点,根据条件,请补充完整图形,并求![]() 的长,直接写出
的长,直接写出![]() 与
与![]() 的长存在的数量关系.
的长存在的数量关系.
![]()
参考答案:
【答案】(1)图见解析;AC=4或8;(2)图见解析;MN=2或4;MN=![]() ;(3)MN=3;MN=
;(3)MN=3;MN=![]() .
.
【解析】
(1)根据点C的位置有两种情况分类讨论,①当点C在点B的左侧时,易求此时AC的长;②当点C在点B的右侧时,易求此时AC的长;
(2)①当点C在点B的左侧时,根据中点的定义,可得:MB=![]() ,NB=
,NB=![]() ,从而求出MN与AC的长度关系,再根据(1)中此时AC的长,即可求出MN的长;②当点C在点B的右侧时,原理同上;
,从而求出MN与AC的长度关系,再根据(1)中此时AC的长,即可求出MN的长;②当点C在点B的右侧时,原理同上;
(3)①当点C在点B的左侧时,根据中点的定义,可得:MC=![]() ,CN=
,CN=![]() ,从而求出MN与AB的长度关系,即可求出MN;②当点C在点B的右侧时,原理同上.
,从而求出MN与AB的长度关系,即可求出MN;②当点C在点B的右侧时,原理同上.
解:(1)根据题意,点C的位置有两种情况
①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() ,
,
∴AC=AB-BC=4;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() ,
,
∴AC=AB+BC=8.
综上所述:AC=4或8;
(2)①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MB=![]() ,NB=
,NB=![]()
∴MN=MB-NB=![]() -
-![]() ==
==![]() =
=![]()
由(1)可知:此时AC=4
∴MN=![]() =2;
=2;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MB=![]() ,NB=
,NB=![]()
∴MN=MB+NB=![]() +
+![]() ==
==![]() =
=![]()
由(1)可知:此时AC=8
∴MN=![]() =4;
=4;
综上所述:MN=2或4;MN=![]() ;
;
(3)①当点C在点B的左侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MC=![]() ,CN=
,CN=![]()
∴MN=MC+ CN =![]() +
+![]() ==
==![]() =
=![]() =3;
=3;
②当点C在点B的右侧时,补全图形如下所示
![]()
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴MC=![]() ,CN=
,CN=![]()
∴MN=MC- CN =![]() -
-![]() ==
==![]() =
=![]() =3;
=3;
综上所述:MN=3;MN=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价贵12元,用12000元购进的科普书本数是用9000元购进的文学书本数的
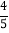 .那么文学书和科普书的单价各是多少元?
.那么文学书和科普书的单价各是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上A点表示数
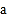 ,B点表示数
,B点表示数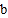 ,
,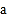 、
、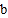 满足|
满足|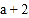 |+|
|+|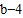 |=0;
|=0;
(1)点A表示的数为_____;点B表示的数为_____;
(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
当t=3时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.
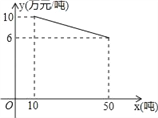
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)求出该反比例函数解析式;
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情況记录如下(单位:
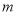 ):
):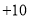 ,
,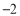 ,
,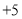 ,
,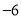 ,
,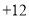 ,
,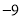 ,
,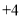 ,
,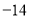 .(假定开始计时时,守门员正好在球门线上)
.(假定开始计时时,守门员正好在球门线上)(1)守门员最后是否回到球门线上?
(2)守门员在这段时间内共跑了多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为15,OC边长为3.

(1)数轴上点A表示的数为 .
(2)将长方形OABC沿数轴水平方向移动,移动后的长方形记为O′A′B′C′(O、A、B、C对应点分别为O′、A′、B′、C′),移动后的长方形O′A′B′C′与原长方形OABC重叠部分的周长记为L.
①当L=10时,移动的距离为 ;
②当L恰好等于原长方形OABC周长的一半时,数轴上点A′表示的数为 .
③设点A的移动距离AA′=x.若D为线段AA′的中点,点E在线段OO′上,且OE=
 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
相关试题

