【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
参考答案:
【答案】
(1)
解:设y与x的函数关系式为y=kx+b(k≠0),根据题意得
![]() ,
,
解得 ![]() .
.
故y与x的函数关系式为y=﹣x+150;
(2)
解:根据题意得
(﹣x+150)(x﹣20)=4000,
解得x1=70,x2=100>90(不合题意,舍去).
故该批发商若想获得4000元的利润,应将售价定为70元;
(3)
解:w与x的函数关系式为:
w=(﹣x+150)(x﹣20)
=﹣x2+170x﹣3000
=﹣(x﹣85)2+4225,
∵﹣1<0,
∴当x=85时,w值最大,w最大值是4225.
∴该产品每千克售价为85元时,批发商获得的利润w(元)最大,此时的最大利润为4225元.
【解析】(1)根据图表中的各数可得出y与x成一次函数关系,从而结合图表的数可得出y与x的关系式.(2)根据想获得4000元的利润,列出方程求解即可;(3)根据批发商获得的总利润w(元)=售量×每件利润可表示出w与x之间的函数表达式,再利用二次函数的最值可得出利润最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二维码已经给我们的生活带来了很大方便,它是由大小相同的黑白两色的小正方形(如图中C型黑白一样)按某种规律组成的一个大正方形。现有25×25格式的正方形如图,角上是三个7×7的A型大黑白相间正方形,中间右下有一个5×5的B型黑白相间正方形((A,B型均由C型黑白两色小正方形组成),除这4个正方形外,其他的C型小正方形黑色块数正好是白色块数的3倍多53块,则该25×25格式的二维码中除去A、B型后,有__块C型白色小正方形,整个二维码中共有__块C型白色小正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.
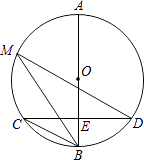
(1)判断BC、MD的位置关系,并说明理由;
(2)若AE=16,BE=4,求线段CD的长;
(3)若MD恰好经过圆心O,求∠D的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.

(1)求圆的半径和点D的坐标;
(2)点A的坐标是 , 点B的坐标是 , sin∠ACB;
(3)求经过C、A、B三点的抛物线解析式;
(4)设抛物线的顶点为F,证明直线FA与⊙D相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x﹣3的图象如图所示,下列说法中错误的是( )
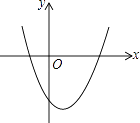
A.函数图象与y轴的交点坐标是(0,﹣3)
B.顶点坐标是(1,﹣3)
C.函数图象与x轴的交点坐标是(3,0)、(﹣1,0)
D.当x<0时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=15,ab=5,求小红家这块L形菜地的面积.

相关试题

