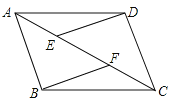
【题目】如图,在ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
参考答案:
【答案】(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;(2)证明见试题解析.
【解析】
试题分析:(1)根据平行四边形的性质得出AB=CD,AD=CB,AB∥CD,AD∥CB,进一步得到∠BAF=∠DCE,∠DAE=∠BCF,由SSS证明△ABC≌△CDA;由SAS证明△ABF≌△CDE;由SAS证明△ADE≌△CBF(SAS);
(2)由△ABF≌△△CDE,得出∠AFB=∠CED,即可证出DE∥BF.
试题解析:(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;理由如下:
∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,AB∥CD,AD∥CB,∴∠BAF=∠DCE,∠DAE=∠BCF,在△ABC和△CDA中,∵AB=CD,CB=AD,AC=CA,∴△ABC≌△CDA(SSS);
∵AE=CF,∴AF=CE,在△ABF和△CDE中,∵AB=CD,∠BAF=∠DCE,AF=CE,∴△ABF≌△CDE(SAS);
在△ADE和△CBF中,∵AD=CB,∠DAE=∠BCF,AE=CF,∴△ADE≌△CBF(SAS).
(2)∵△ABF≌△△CDE,∴∠AFB=∠CED,∴DE∥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△A′B′C′,相似比为1:3,则△ABC与△A′B′C′的面积之比为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).
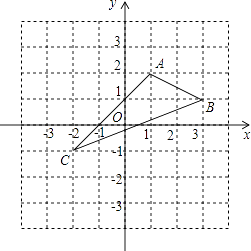
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1 .
(2)写出点A1 , B1 , C1的坐标(直接写答案). A1
B1
C1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】①如图1:A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点的位置(保留作图痕迹).
②如图2:某地有两个工厂M、N和两条相交叉的公路a,b现计划修建一座物资仓库,希望仓库到两个工厂的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.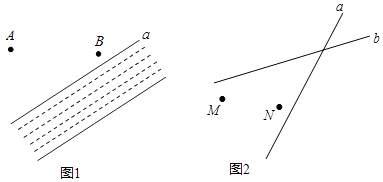
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(﹣3a)2=3a2
B.a6÷a3=a2
C.﹣3(a﹣1)=3﹣3a
D.aa2=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:2(﹣3x2y+xy)﹣[2xy﹣4(xy﹣
 x2y)+x2y],其中x、y满足|x﹣3|+(y+
x2y)+x2y],其中x、y满足|x﹣3|+(y+  )2=0.
)2=0.
相关试题

