【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() 的图像与
的图像与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.

(1)求点![]() 坐标和点
坐标和点![]() 坐标;
坐标;
(2)点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 为坐标原点,点
为坐标原点,点![]() 在第二象限,且四边形
在第二象限,且四边形![]() 为菱形,求点
为菱形,求点![]() 坐标;
坐标;
(3)在(2)的条件下,点![]() 为平面直角坐标系中一点,以
为平面直角坐标系中一点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请直接写出所有满足条件的
为顶点的四边形是平行四边形,请直接写出所有满足条件的![]() 点坐标.
点坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)D
;(2)D![]() ;(3)
;(3)![]() ;
;![]() ;
;![]()
【解析】
(1)分别令x与y为0,求出对应y与x的值,即可确定出A与B的坐标;
(2)设点![]() 坐标为
坐标为![]() ,根据题意知
,根据题意知![]() ,根据两点之间的距离公式即可求得点
,根据两点之间的距离公式即可求得点![]() 的坐标,利用轴对称的性质即可求得点
的坐标,利用轴对称的性质即可求得点![]() 的坐标;
的坐标;
(3)过A作BD的平行线![]() ,过D作AB的平行线
,过D作AB的平行线![]() ,过B作AD的平行线
,过B作AD的平行线![]() ,分别相交于
,分别相交于![]() 、
、![]() 、
、![]() ,利用待定系数法分别求得直线
,利用待定系数法分别求得直线![]() 、
、![]() 、
、![]() 的解析式,再求直线的交点坐标即可求解.
的解析式,再求直线的交点坐标即可求解.
(1)当![]() 时,得
时,得![]() ,解得:
,解得:![]()
∴点B的坐标为(0,4),
当![]() 时,得
时,得![]() ,解得:
,解得:![]()
∴点A的坐标为(2,0);
(2)∵点![]() 是线段
是线段![]() 上,
上,
∴设点![]() 坐标为
坐标为![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
则![]() ,
,
解得![]() .
.
∴点![]() 坐标为
坐标为![]() .
.
∵点![]() 、
、![]() 关于
关于![]() 轴对称,
轴对称,
∴点![]() 坐标为
坐标为![]() ;
;
(3)过A作BD的平行线![]() ,过D作AB的平行线
,过D作AB的平行线![]() ,过B作AD的平行线
,过B作AD的平行线![]() ,分别相交于
,分别相交于![]() 、
、![]() 、
、![]() ,如图:
,如图:

∵点A、B、D的坐标分别为(2,0),(0,4),(-1,2),
设BD的解析式为![]() ,
,
把点D的坐标 (-1,2)代入得:![]() ,
,
解得:![]() ,
,
∴设直线![]() 的解析式为
的解析式为![]() ,
,
把点A的坐标 (2,0)代入得:![]() ,
,
解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
同理可求得直线![]() 、
、![]() 的解析式分别为
的解析式分别为![]() 、
、![]() ,
,
联立![]() 、
、![]() 得:
得:![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为(1,-2);
的坐标为(1,-2);
联立![]() 、
、![]() 得:
得: ,解得
,解得![]() ,
,
∴点![]() 的坐标为(3,2);
的坐标为(3,2);
联立![]() 、
、![]() 得:
得: ,解得
,解得![]() ,
,
∴点![]() 的坐标为(-3,6);
的坐标为(-3,6);
综上,所有满足条件的![]() 点坐标为(1,-2),(3,2),(-3,6);
点坐标为(1,-2),(3,2),(-3,6);
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣
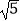 ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2 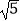 ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2 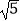 .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=
 位于第一象限的图象上,则k的值为( )
位于第一象限的图象上,则k的值为( )
A.9
B.9
C.3
D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A.S3>S4>S6
B.S6>S4>S3
C.S6>S3>S4
D.S4>S6>S3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中, ,
, ,
, .
.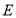 是边
是边 的中点,联结
的中点,联结 、
、 ,且
,且 .设
.设 ,
, .
.

(1)如果
 ,求
,求 的长;
的长;(2)求
 关于
关于 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围;
的取值范围;(3)联结
 .如果
.如果 是以边
是以边 为腰的等腰三角形,求
为腰的等腰三角形,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 .

相关试题

