搜索
【题目】如图，⊙
是
的内切圆，切点分别为
、
、
， 
， 
．
（
）求
的度数．
（
）求
的度数．
参考答案：
【答案】（
）
（
）
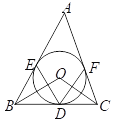
【解析】试题分析：（1）由切线长定理可知BO，CO分别是∠ABC和∠ACB的角平分线，则∠OBC和∠OCB的度数可求出，进而可求出∠BOC的度数；
（2）连接OE，OF．由三角形内角和定理可求得∠A=50°，由切线的性质可知：∠OFA=90°，∠OEA=90°，从而得到∠A+∠EOF=180°，故可求得∠EOF=130°由圆周角定理可求得∠EDF=65°．
试题解析：解：（1）∵⊙O是△ABC的内切圆，切点分别为D、E、F，∴BO，CO分别是∠ABC和∠ACB的角平分线，∴∠OBC=
∠ABC=30°，∠OCB=
∠ACB=35°，∴∠BOC=180°﹣30°﹣35°=115°；
（2）如图所示；连接OE，OF．
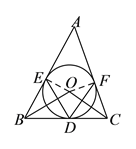
∵∠ABC=60°，∠ACB=70°，∴∠A=180°﹣60°﹣70°=50°．
∵AB是圆O的切线，∴∠OFA=90°．
同理∠OEA=90°，∴∠A+∠EOF=180°，∴∠EOF=130°，∴∠EDF=65°．
-
科目： 来源： 题型：
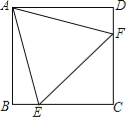
查看答案和解析>>【题目】如图，正方形ABCD边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB延长线于点F，则EF的长为__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=
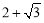．其中正确的序号是 （把你认为正确的都填上）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形
的对角线交于点
点
，
分别在
，
上（
）且
，
，
的延长线交于点
，
，的延长线交于点
，连接
.（1）求证：
.（2）若正方形
的边长为4，为
的中点，求的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将三角形ABC向右平移5个单位长度，再向上平移3个单位长度请回答下列问题：
（1）平移后的三个顶点坐标分别为：A1 ，B1 ，C1 ；
（2）画出平移后三角形A1B1C1；
（3）求三角形ABC的面积．
-
科目： 来源： 题型：
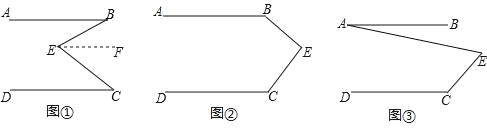
查看答案和解析>>【题目】（1）问题发现：如图①，直线AB∥CD，E是AB与CD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC．
请把下面的证明过程补充完整：
证明：过点E作EF∥AB，
∵AB∥DC（已知），EF∥AB（辅助线的作法），
∴EF∥DC（ ）
∴∠C=∠CEF．（ ）
∵EF∥AB，∴∠B=∠BEF（同理），
∴∠B+∠C= （等式性质）
即∠B+∠C=∠BEC．
（2）拓展探究：如果点E运动到图②所示的位置，其他条件不变，求证：∠B+∠C=360°﹣∠BEC．
（3）解决问题：如图③，AB∥DC，试写出∠A、∠C、∠AEC的数量关系 ．（直接写出结论，不用写计算过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE="10," 求直角梯形ABCD的面积．
相关试题
