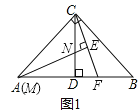
【题目】如图:已知△ABC中,CA=CB,CD⊥AB于D点,点M为线段AC上一动点,线段MN交DC于点N,且∠BAC=2∠CMN,过点C作CE⊥MN交MN延长线于点E,交线段AB于点F,探索![]() 的值.
的值.
(1)若∠ACB=90°,点M与点A重合(如图1)时:①线段CE与EF之间的数量关系是 ;②![]() = ;
= ;
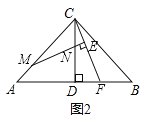
(2)在(1)的条件下,若点M不与点A重合(如图2),请猜想写出![]() 的值,并证明你的猜想
的值,并证明你的猜想
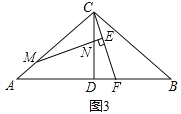
(3)若∠ACB≠90°,∠CAB=![]() ,其他条件不变,请直接写出
,其他条件不变,请直接写出![]() 的值(用含有
的值(用含有![]() 的式子表示)
的式子表示)
参考答案:
【答案】(1)①CE=EF,② ![]() ;(2)
;(2)![]() =
=![]() ,理由见解析;(3)
,理由见解析;(3)![]() =
=![]() .
.
【解析】(1)、根据等腰三角形的三线合一定理得出点E为CF的中点,从而得出答案;(2)、过点M作MQ//AB交CD于点P,交CF于点Q,根据等腰三角形、直角三角形的性质得出△MPN和△CPQ全等,从而得出CE=EQ ,MC=MQ,即CE=![]() CQ=
CQ=![]() MN;(3)、如图3,同(1)、(2)可得CE=
MN;(3)、如图3,同(1)、(2)可得CE= ![]() CQ,易证△MPN~△CPQ,则有
CQ,易证△MPN~△CPQ,则有![]() ,即
,即![]() .
.
(1)、①CE=EF;② ![]() ;
;
(2)、![]() =
=![]()
理由如下:如图2所示:过点M作MQ//AB交CD于点P,交CF于点Q,
则有∠CMP=∠BAC=45°, ∴CP=MP,
∵∠BAC=2∠CMN, ∴∠CMP=2∠CMN, ∴∠CMN=∠NMP=22.5°,∵CE⊥MN,
∴∠CEM=∠QEM=90°,∴CE=EQ (三线合一),∵CD⊥AB, MQ//AB,
∴CD⊥MQ,∴∠MPN=∠CPQ=90°,又∵∠NCE+∠CNE=∠NCE+∠CQN=90°,
∴∠CQN=∠CNE=∠MNP,又CP=MP,∴△MPN![]() △CPQ,∴CE=EQ ,MC=MQ,
△CPQ,∴CE=EQ ,MC=MQ,
∴CE=![]() CQ=
CQ=![]() MN,∴
MN,∴![]() =
=![]() ;
;
(3)、![]() =
=![]() .
.
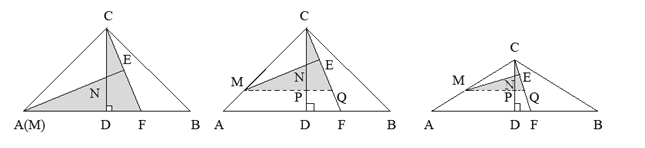
图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
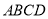 是矩形,点
是矩形,点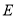 在线段
在线段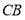 的延长线上,连接
的延长线上,连接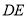 交
交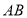 于点
于点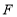 ,
,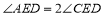 ,点
,点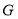 是
是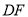 的中点.若
的中点.若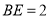 ,
,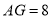 ,则
,则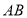 的长为__.
的长为__.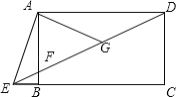
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班的全体同学排成一列步行去市博物馆参加科技活动,小涛担任通讯员.在队伍中,小涛先数了一下他前后的人数,发现前面的人数是后面人数的2倍,他往前超了8名同学后,发现前面的人数和后面的人数一样.
(1)七年级(1)班有多少名同学?
(2)这些同学要过一座长60米的大桥,安全起见,相邻两个同学间保持相同的固定距离,队伍前进速度为1.2米/秒,从第一名同学刚上桥到全体通过大桥用了90秒,则队伍的全长为多少米?
(3)在(2)的条件下,排在队尾的小刚想把一则通知送到队伍最前的小婷手中,若小刚从队尾追赶小婷的速度是4.2米/秒,他能在15秒内追上小婷吗?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店中销售水果时采用了三种组合搭配的方式进行销售,甲种搭配是:2千克A水果,4千克B水果;乙种搭配是:3千克A水果,8千克B水果,1千克C水果;丙种搭配是:2千克A水果,6千克B水果,1千克C水果;如果A水果每千克售价为2元,B水果每千克售价为1.2元,C水果每千克售价为10元,某天,商店采用三种组合搭配的方式进行销售后共得销售额441.2元,并且A水果销售额116元,那么C水果的销售额是______元.
-
科目: 来源: 题型:
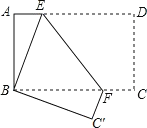
查看答案和解析>>【题目】如图,长方形纸片 ABCD,AD∥BC,将长方形纸片折叠, 使点 D 与点 B 重合,点 C 落在点 C'处,折痕为 EF.
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE 的度数.
(3)若 AB=4,AD=8,求 AE 的长.
-
科目: 来源: 题型:
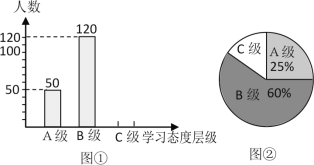
查看答案和解析>>【题目】初中生对待学习的态度一直是教育工作者关注的问题之一.为此某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该市近20000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?
相关试题

