【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 于点
于点![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.若
的中点.若![]() ,
,![]() ,则
,则![]() 的长为__.
的长为__.
参考答案:
【答案】![]()
【解析】
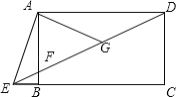
根据直角三角形斜边上的中线等于斜边的一半可得AG=DG,然后根据等边对等角的性质可得∠ADG=∠DAG,再结合两直线平行,内错角相等可得∠ADG=∠CED,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AGE=2∠ADG,从而得到∠AED=∠AGE,再利用等角对等边的性质得到AE=AG,然后利用勾股定理列式计算即可得解.
解:∵四边形ABCD是矩形,点G是DF的中点,
∴AG=DG,
∴∠ADG=∠DAG,
∵AD∥BC,
∴∠ADG=∠CED,
∴∠AGE=∠ADG+∠DAG=2∠CED,
∵∠AED=2∠CED,
∴∠AED=∠AGE,
∴AE=AG=8,
在Rt△ABE中,AB=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
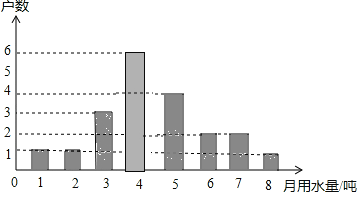
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,图1中面积为1的正方形有9个,图2中面积为1的正方形有14个,
 ,按此规律,图12中面积为1的正方形的个数为
,按此规律,图12中面积为1的正方形的个数为

A.64B.60C.54D.50
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
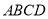 中,
中,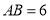 ,点
,点 在边
在边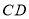 上,且
上,且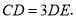 将
将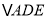 沿
沿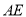 对折至
对折至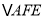 ,延长
,延长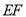 交边
交边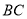 于点
于点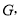 连结
连结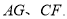 下列结论:①
下列结论:①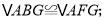 ②
②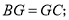 ③
③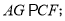 ④
④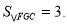
其中正确结论的个数是 ( )
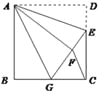
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班的全体同学排成一列步行去市博物馆参加科技活动,小涛担任通讯员.在队伍中,小涛先数了一下他前后的人数,发现前面的人数是后面人数的2倍,他往前超了8名同学后,发现前面的人数和后面的人数一样.
(1)七年级(1)班有多少名同学?
(2)这些同学要过一座长60米的大桥,安全起见,相邻两个同学间保持相同的固定距离,队伍前进速度为1.2米/秒,从第一名同学刚上桥到全体通过大桥用了90秒,则队伍的全长为多少米?
(3)在(2)的条件下,排在队尾的小刚想把一则通知送到队伍最前的小婷手中,若小刚从队尾追赶小婷的速度是4.2米/秒,他能在15秒内追上小婷吗?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

-
科目: 来源: 题型:
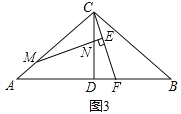
查看答案和解析>>【题目】如图:已知△ABC中,CA=CB,CD⊥AB于D点,点M为线段AC上一动点,线段MN交DC于点N,且∠BAC=2∠CMN,过点C作CE⊥MN交MN延长线于点E,交线段AB于点F,探索
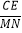 的值.
的值.(1)若∠ACB=90°,点M与点A重合(如图1)时:①线段CE与EF之间的数量关系是 ;②
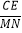 = ;
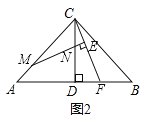
= ;(2)在(1)的条件下,若点M不与点A重合(如图2),请猜想写出
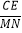 的值,并证明你的猜想
的值,并证明你的猜想(3)若∠ACB≠90°,∠CAB=
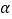 ,其他条件不变,请直接写出
,其他条件不变,请直接写出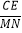 的值(用含有
的值(用含有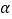 的式子表示)
的式子表示)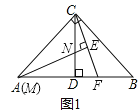
相关试题

