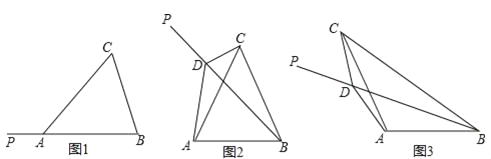
【题目】如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
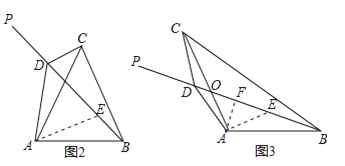
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
参考答案:
【答案】(1)∠ACD=∠ABD,BD=CD+AD;(2)详见解析;(3)BD+CD=![]() AD.
AD.
【解析】试题分析:(1)如图2,根据已知条件易证∠CDB=∠BAC=60°,可得A、B、C、D四点共圆,根据圆周角定理可得∠ACD=∠ABD;在BP上截取BE=CD,连接AE.利用SAS证明△DCA≌△EBA,得出AD=AE,∠DAC=∠EAB,再证明△ADE是等边三角形,得到DE=AD,从而得出BD=CD+AD.
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.根据两角对应相等的两三角形相似可证△DOC∽△AOB,所以∠DCA=∠EBA.再利用SAS证明△DCA≌△EBA,得出AD=AE,∠DAC=∠EAB.由∠CAB=∠CAE+∠EAB=120°,得出∠DAE=120°,根据等腰三角形的性质及三角形内角和定理求出∠ADE=∠AED=![]() =30°.在Rt△ADF,利用锐角三角函数得到DF=
=30°.在Rt△ADF,利用锐角三角函数得到DF=![]() AD,所以DE=2DF=
AD,所以DE=2DF=![]() AD,从而得出BD=DE+BE=
AD,从而得出BD=DE+BE=![]() AD+CD,即BD﹣CD=
AD+CD,即BD﹣CD=![]() AD;
AD;
(3)同(2)证明可以得出BD+CD=![]() AD.
AD.
试题解析:解:(1)如图2,∵∠CDP=120°,
∴∠CDB=60°,
∵∠BAC=60°,
∴∠CDB=∠BAC=60°,
∴A、B、C、D四点共圆,
∴∠ACD=∠ABD.
在BP上截取BE=CD,连接AE.
在△DCA与△EBA中,
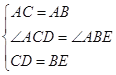 ,
,
∴△DCA≌△EBA(SAS),
∴AD=AE,∠DAC=∠EAB,
∵∠CAB=∠CAE+∠EAB=60°,
∴∠DAE=60°,
∴△ADE是等边三角形,
∴DE=AD.
∵BD=BE+DE,
∴BD=CD+AD.
故答案为∠ACD=∠ABD,BD=CD+AD;
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.
∵∠CDP=60°,
∴∠CDB=120°.
∵∠CAB=120°,
∴∠CDB=∠CAB,
∵∠DOC=∠AOB,
∴△DOC∽△AOB,
∴∠DCA=∠EBA.
在△DCA与△EBA中,
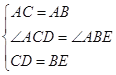 ,
,
∴△DCA≌△EBA(SAS),
∴AD=AE,∠DAC=∠EAB.
∵∠CAB=∠CAE+∠EAB=120°,
∴∠DAE=120°,
∴∠ADE=∠AED=![]() =30°.
=30°.
∵在Rt△ADF中,∠ADF=30°,
∴DF=![]() AD,
AD,
∴DE=2DF=![]() AD,
AD,
∴BD=DE+BE=![]() AD+CD,
AD+CD,
∴BD﹣CD=![]() AD;
AD;
(3)BD+CD=![]() AD.
AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:

(1)∠1和∠3是直线__________被直线__________所截得的__________;
(2)∠1和∠4是直线__________被直线__________所截得的__________;
(3)∠B和∠2是直线__________被直线__________所截得的__________;
(4)∠B和∠4是直线__________被直线__________所截得的__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
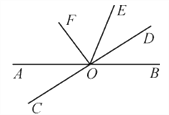
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=(3﹣k)x+18﹣2k2的图象经过原点,则k的值为( )
A. 3 B. ﹣3 C. ±3 D. 任何实数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=
 ,求DE的长.
,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数x满足x2﹣2x﹣1=0,则2x3﹣7x2+4x﹣2017= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国的陆地面积约为9600000km2 , 将这个数用科学记数法可表示为( )
A.0.96×107km2
B.960×104km2
C.9.6×106km2
D.9.6×105km2
相关试题

