【题目】利用如图1的二维码可以进行身份识别,某校模仿二维码建立了一个七年级学生身份识别系统,图2是七年级某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20+1.如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20+1=6表示该生为6班学生.则该系统最多能识别七年级的班级数是___个.

参考答案:
【答案】16.
【解析】
该系统最多能识别七年级的班级数是a×![]() +b×
+b×![]() +c×
+c×![]() +d×
+d×![]() +1的最大值,由于a,b,c,d的取值只能是0或1,所以当a=b=c=d=1时,序号有最大值.
+1的最大值,由于a,b,c,d的取值只能是0或1,所以当a=b=c=d=1时,序号有最大值.
当a=b=c=d=1时,
a×23+b×22+c×21+d×20+1
=1×23+1×22+1×21+1×20+1
=8+4+2+1+1
=16.
故答案为16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年9月,某手机公司发布了新款智能手机,为了调查某小区业主对该款手机的购买意向,该公司在某小区随机对部分业主进行了问卷调查,规定每人只能从A类(立刻去抢购)、B类(降价后再去买)、C类(犹豫中)、D类(肯定不买)这四类中选一类,并制成了以下两幅不完整的统计图,由图中所给出的信息解答下列问题:
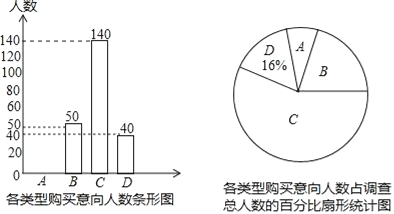
(1)扇形统计图中B类对应的百分比为 %,请补全条形统计图;
(2)若该小区共有4000人,请你估计该小区大约有多少人立刻去抢购该款手机.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )

A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成。
(1)若围成的面积为180m2,试求出自行车车棚的长和宽;
(2)能围成的面积为200m2自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b=
 ,
,例如:1⊕(﹣3)=
 =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,(x2+1)⊕(x﹣1)=
 (因为x2+1>0)
(因为x2+1>0)参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>
 ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在正方形
 中,
中,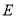 、
、 分别是
分别是 、
、 边上的点,
边上的点, ,连接
,连接 ,
, 交于点
交于点 .求证:
.求证: 且
且 ;
;(2)如图②,若点
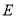 、
、 分别在
分别在 、
、 的延长线上,且
的延长线上,且 ,(1)中的结论是否成立?如果成立,请说明理由;
,(1)中的结论是否成立?如果成立,请说明理由;(3)如图③,在图②的基础上连接
 、
、 、
、 、
、 、
、 、
、 分别是
分别是 、
、 、
、 、
、 的中点,请直接写出四边形
的中点,请直接写出四边形 的形状.
的形状.
相关试题

