搜索
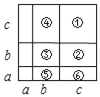
【题目】若a、b、c是正数，下列各式，从左到右的变形不能用如图验证的是（ ）
A. （b+c）2＝b2+2bc+c2
B. a（b+c）＝ab+ac
C. （a+b+c）2＝a2+b2+c2+2ab+2bc+2ac
D. a2+2ab＝a（a+2b）
参考答案：
【答案】D
【解析】
通过几何图形面积之间的数量关系完全平方公式或其他等式作出几何解释即可.
依据①②③④四部分的面积可得，（b+c）2＝b2+2bc+c2，故A能验证；
依据⑤⑥两部分的面积可得，a（b+c）＝ab+ac，故B能验证；
依据整个图形的面积可得，（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac，故C能验证；
图中不存在长为a+2b，宽为a的长方形，故D选项不能验证；
故选：D．
-
科目： 来源： 题型：
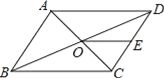
查看答案和解析>>【题目】如图，平行四边形ABCD的周长为36，对角线AC，BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2016年9月，某手机公司发布了新款智能手机，为了调查某小区业主对该款手机的购买意向，该公司在某小区随机对部分业主进行了问卷调查，规定每人只能从A类（立刻去抢购）、B类（降价后再去买）、C类（犹豫中）、D类（肯定不买）这四类中选一类，并制成了以下两幅不完整的统计图，由图中所给出的信息解答下列问题：
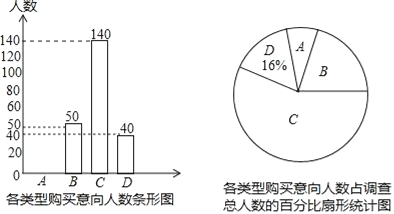
（1）扇形统计图中B类对应的百分比为 %，请补全条形统计图；
（2）若该小区共有4000人，请你估计该小区大约有多少人立刻去抢购该款手机．
-
科目： 来源： 题型：
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别，某校模仿二维码建立了一个七年级学生身份识别系统，图2是七年级某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0．将第一行数字从左到右依次记为a，b，c，d，那么可以转换为该生所在班级序号，其序号为a×23+b×22+c×21+d×20+1．如图2第一行数字从左到右依次为0，1，0，1，序号为0×23+1×22+0×21+1×20+1＝6表示该生为6班学生．则该系统最多能识别七年级的班级数是___个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，学校准备在教学楼后面搭建一简易矩形自行车车棚，一边利用教学楼的后墙（可利用的墙长为19m），另外三边利用学校现有总长38m的铁栏围成。
（1）若围成的面积为180m2，试求出自行车车棚的长和宽；
（2）能围成的面积为200m2自行车车棚吗？如果能，请你给出设计方案；如果不能，请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】设a，b是任意两个实数，规定a与b之间的一种运算“⊕”为：a⊕b=
，例如：1⊕（﹣3）=
=﹣3，（﹣3）⊕2=（﹣3）﹣2 =﹣5，（x2+1）⊕（x﹣1）=
（因为x2+1＞0）参照上面材料，解答下列问题：
（1）2⊕4= ，（﹣2）⊕4= ；
（2）若x＞
，且满足（2x﹣1）⊕（4x2﹣1）=（﹣4）⊕（1﹣4x），求x的值．
相关试题
