搜索
【题目】（1）如图①，在正方形
中，
、
分别是
、
边上的点，
，连接
，
交于点
．求证：
且
；
（2）如图②，若点、分别在
、
的延长线上，且，（1）中的结论是否成立？如果成立，请说明理由；
（3）如图③，在图②的基础上连接
、
、
、
、
、
分别是、、
、
的中点，请直接写出四边形
的形状．
参考答案：
【答案】（1）证明见解析；（2）成立，理由见解析；（3）正方形．
【解析】
（1）首先由正方形的性质判定
，得出
，然后进行等量转换即可得出
；
（2）首先由正方形的性质得出
，判定，得出，然后进行等量转换即可得出；
（3）由中位线定理和（2）中的结论即可判定.
（1）∵四边形
是正方形
∴
∵
∴
即
∴
∴
∴
∵
∴
∴
∴
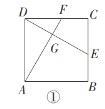
（2）（1）中的结论成立
∵四边形是正方形
∴
又∵
∴
即
∴
∴
∴
∵
∴
∴
∴
（3）四边形
是正方形
∵
、
、
、
分别是
、
、
、
的中点，
∴
由（2）结论，得，
∴
，∠HMN=∠MNP=∠NPH=∠PHM=90°
∴四边形是正方形
-
科目： 来源： 题型：
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别，某校模仿二维码建立了一个七年级学生身份识别系统，图2是七年级某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0．将第一行数字从左到右依次记为a，b，c，d，那么可以转换为该生所在班级序号，其序号为a×23+b×22+c×21+d×20+1．如图2第一行数字从左到右依次为0，1，0，1，序号为0×23+1×22+0×21+1×20+1＝6表示该生为6班学生．则该系统最多能识别七年级的班级数是___个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，学校准备在教学楼后面搭建一简易矩形自行车车棚，一边利用教学楼的后墙（可利用的墙长为19m），另外三边利用学校现有总长38m的铁栏围成。
（1）若围成的面积为180m2，试求出自行车车棚的长和宽；
（2）能围成的面积为200m2自行车车棚吗？如果能，请你给出设计方案；如果不能，请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】设a，b是任意两个实数，规定a与b之间的一种运算“⊕”为：a⊕b=
，例如：1⊕（﹣3）=
=﹣3，（﹣3）⊕2=（﹣3）﹣2 =﹣5，（x2+1）⊕（x﹣1）=
（因为x2+1＞0）参照上面材料，解答下列问题：
（1）2⊕4= ，（﹣2）⊕4= ；
（2）若x＞
，且满足（2x﹣1）⊕（4x2﹣1）=（﹣4）⊕（1﹣4x），求x的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】某商店经销一种成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克．若销售价每涨1元，则月销售量减少10千克．
（1）要使月销售利润达到最大，销售单价应定为多少元？
（2）要使月销售利润不低于8000元，请结合图象说明销售单价应如何定？
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形证明了勾股定理，如图所示的矩形由两个这样的图形拼成，若a=3，b=4，则该矩形的面积为（ ）
A. 20 B. 24 C.
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ACB和△ECD都是等腰直角三角形，CA＝CB，CE＝CD，△ACB的顶点A在△ECD的斜边DE上
（1）求证：AE2+AD2＝2AC2；
（2）如图2，若AE＝2，AC＝2
，点F是AD的中点，直接写出CF的长是 ．
相关试题
