【题目】现有A,B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5,它们除数字外完全一样.
(1)随机地从A中抽取一张,求抽到数字为2的概率;
(2)随机地分别从A、B中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果.现制定这样一个游戏规则:若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?若不公平,你认为怎样制定游戏规则,对甲乙双方才公平?
参考答案:
【答案】
(1)解:∵A中三张分别写有数字2,4,6,
∴抽到数字为2的概率P= ![]()
(2)解:由题意画出树状图如下:

一共有6种情况,
甲获胜的情况有4种,甲获胜的概率P= ![]() =
= ![]() ,
,
乙获胜的情况有2种,乙获胜的概率P= ![]() =
= ![]() ,
,
所以,这样的游戏规则对甲乙双方不公平.
游戏规则改为:
若所选出的两数字之积为3的倍数,记甲2分;否则记乙3分;谁先积满6n分(n为正整数)就获胜,这样对甲乙双方都公平
【解析】(1)根据概率的定义列式计算即可;(2)画出树状图,然后根据概率的意义分别求出甲、乙获胜的概率,从而得解;根据游戏的公平性进行判断即可得到游戏规则.
【考点精析】本题主要考查了列表法与树状图法和概率公式的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△AEC=S△ABC,其中正确结论有( )个.
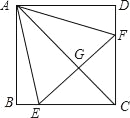
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的解析式为y=﹣x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(﹣1,m),且与x轴交于点A,
(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
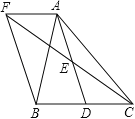
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由大小相同的小立方块搭成的几何体如左图:
(1)请在下面的方格中画出该几何体从上面和从左面看的两个图形.
(2)若现在你手头上还有一些相同的小立方块,如果保持从上面看和从左面看所得图形不变,则在左图中最多可以再添加 个小立方块.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学计划从一文体公司购买甲,乙两种型号的小黑板,经洽谈,购买一块甲型小黑板比购买一块乙型小黑板多用20元,且购买2块甲型小黑板和3块乙型小黑板共需440元.
(1)求购买一块甲型小黑板、一块乙型小黑板各需多少元?
(2)根据该中学实际情况,需从文体公司购买甲,乙两种型号的小黑板共60块,要求购买甲,乙两种型号小黑板的总费用不超过5240元.并且购买甲型小黑板的数量不小于购买乙型小黑板数量的 .则该中学从文体公司购买甲,乙两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从文体公司购买甲,乙两种型号的小黑板有哪几种方案?哪种方案的总费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2
 ,
, .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

相关试题

