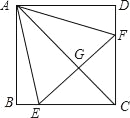
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△AEC=S△ABC,其中正确结论有( )个.
A. 5 B. 4 C. 3 D. 2
参考答案:
【答案】C
【解析】
试题∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴①说法正确;
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴△ECF是等腰直角三角形,
∴∠CFE=45°
∴∠AFD=75°
∴∠DAF=15°
∴②正确;
∵AC是正方形ABCD的对角线,∴∠BCA=45°
∴AC⊥EF
又CE=CF
∴AC垂直平分EF,
∴③正确;
在AD上取一点G,连接FG,使AG=GF,

则∠DAF=∠GFA=15°,
∴∠DGF=2∠DAF=30°,
设DF=1,则AG=GF=2,DG=![]() ,
,
∴AD=CD=2+![]() ,CF=CE=CD-DF=1+
,CF=CE=CD-DF=1+![]() ,
,
∴EF=![]() CF=
CF=![]() +
+![]() ,而BE+DF=2,
,而BE+DF=2,
∴④说法错误;
∵S△ABE+S△ADF=2S△ABE=2×![]() AD×DF=2+
AD×DF=2+![]() ,
,
S△CEF=![]() CE×CF=
CE×CF=![]() ,
,
∴⑤正确
故选B.
考点: 1.正方形的性质;2.全等三角形的判定与性质;3.等边三角形的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.

(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一果农贩卖的西红柿,其重量与价钱成一次函数关系.小华向果农买一竹篮的西红柿,含竹篮称得总重量为15公斤,付西红柿的钱26元,若再加买0.5公斤的西红柿,需多付1元,则空竹篮的重量为多少?( )
A. 1.5 B. 2 C. 2.5 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某星期天下午,小强和同学小颖相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小颖到了后两人一起乘公共汽车回学校,图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系,下列说法中错误的是( )
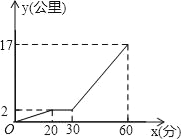
A. 小强乘公共汽车用了20分钟 B. 小强在公共汽车站等小颖用了10分钟
C. 公共汽车的平均速度是30公里/小时 D. 小强从家到公共汽车站步行了2公里
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的解析式为y=﹣x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(﹣1,m),且与x轴交于点A,
(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
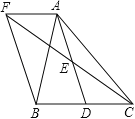
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有A,B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5,它们除数字外完全一样.
(1)随机地从A中抽取一张,求抽到数字为2的概率;
(2)随机地分别从A、B中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果.现制定这样一个游戏规则:若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?若不公平,你认为怎样制定游戏规则,对甲乙双方才公平?
相关试题

