搜索
【题目】如图是一个多面体的表面展开图,每个面上都标注了字母(字母在多面体的外表面),请根据要求回答问题.
(1)如果D面在多面体的左面,那么F面在哪里?
(2)B面和哪一面是相对的面?
(3)如果C面在前面,从上面看到的是D面,那么从左面能看到哪一面?
参考答案：
【答案】(1)D面在左面,所以F面在右面.(2)B面和E面是相对的面.(3)C面在前面,从上面看到的是D面,所以从左面能看到B面.
【解析】
利用长方体及其表面展开图的特点解题．这是一个正方体的平面展开图，共有六个面，其中面“A”与面“C”相对，面“B”与面“E”相对，“D”与面“F”相对．
解：这是一个正方体的平面展开图，共有六个面，其中面“A”与面“C”相对，面“B”与面“E”相对，“D”与面“F”相对．则
（1）∵面“D”与面“F”相对，∴D面是长方体的左面时，F面在右面；
（2）由图可知，B面和E面是相对的面；
（3）由图可知，C面在前面,从上面看到的是D面,所以从左面能看到B面.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司在某市五个区投放共享单车供市民使用，投放量的分布及投放后的使用情况统计如下．
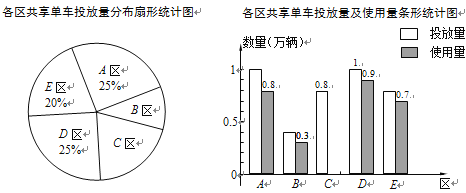
（1）该公司在全市一共投放了 万辆共享单车；
（2）在扇形统计图中，B区所对应扇形的圆心角为 °；
（3）该公司在全市投放的共享单车的使用量占投放量的85%，请计算C区共享单车的使用量并补全条形统计图．
-
科目： 来源： 题型：
查看答案和解析>>【题目】像(
+2)(﹣2)＝1、
＝a(a≥0)、(
+1)(﹣1)＝b﹣1(b≥0)……两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式．例如，与，
+1与﹣1，2
+3与2﹣3等都是互为有理化因式．进行二次根式计算时，利用有理化因式，可以化去分母中的根号．请完成下列问题：(1)化简：
；(2)计算：
；(3)比较
与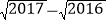
的大小，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD中，AB⊥AC，AB=2，AC=4．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转α°，分别交直线BC、AD于点E、F．
（1）当α= °，四边形ABEF是平行四边形；
（2）在旋转的过程中，从A、B、C、D、E、F中任意4个点为顶点构造四边形．
①α= °，构造的四边形是菱形；
②若构造的四边形是矩形，求出该矩形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用，假定每辆观光车一天内最多只能出租一次，且每辆车的日租金x（元）是5的倍数．发现每天的营运规律如下：当x不超过100元时，观光车能全部租出；当x超过100元时，每辆车的日租金每增加5元，租出去的观光车就会减少1辆．已知所有观光车每天的管理费是1100元．
（1）优惠活动期间，为使观光车全部租出且每天的净收入为正，则每辆车的日租金至少应为多少元？（注：净收入=租车收入﹣管理费）
（2）当每辆车的日租金为多少元时，每天的净收入最多？ -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：
如图①，在平面直角坐标系中，若已知点A（xA，yA）和点C（xC，yC），点M为线段AC的中点，利用三角形全等的知识，有△AMP≌△CMQ，则有PM=MQ，PA=QC，即xM﹣xA=xC﹣xM，yA﹣yM=yM﹣yC，从而有
，即中点M的坐标为（
，
）．
基本知识：
（1）如图①，若A、C点的坐标分别A（﹣1，3）、C（3，﹣1），求AC中点M的坐标；
方法提炼：
（2）如图②，在平面直角坐标系中，ABCD的顶点A、B、C的坐标分别为（﹣1，5）、（﹣2，2）、（3，3），求点D的坐标；
（3）如图③，点A是反比例函数y=
（x＞0）上的动点，过点A作AB∥x轴，AC∥y轴，分别交函数y═
（x＞0）的图象于点B、C，点D是直线y=2x上的动点，请探索在点A运动过程中，以A、B、C、D为顶点的四边形能否为平行四边形，若能，求出此时点A的坐标；若不能，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，AB=2，∠BAD=60°，过点D作DE⊥AB于点E，DF⊥BC于点F．
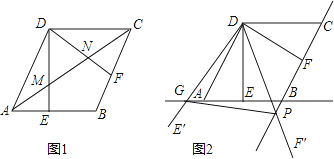
（1）如图1，连接AC分别交DE、DF于点M、N，求证：MN=
AC；
（2）如图2，将△EDF以点D为旋转中心旋转，其两边DE′、DF′分别与直线AB、BC相交于点G、P，连接GP，当△DGP的面积等于3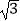
时，求旋转角的大小并指明旋转方向．
相关试题
