【题目】如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm
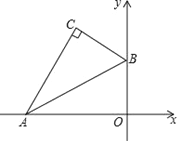
(1)若OB=6cm.①求点C的坐标;②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;
(2)点C与点O的距离的最大值= cm.
参考答案:
【答案】(1)①C(![]() ,9);②
,9);②![]() ;(2)12.
;(2)12.
【解析】试题分析:(1)①过点C作y轴的垂线,垂足为D,利用含30°角的直角三角形的性质解答即可;
②设点A向右滑动的距离为x,则点B向上滑动的距离也为x,利用三角函数和勾股定理进行解答即可;
(2)过C作CE⊥x轴,CD⊥y轴,垂足分别为E,D,得到△ACE∽△BCD,再利用相似三角形的性质解答.
试题解析:(1)①过点C作y轴的垂线,垂足为D,如图1:
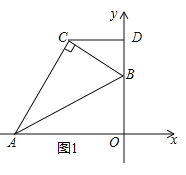
在Rt△AOB中,AB=12,OB=6,则BC=6,∴∠BAO=30°,∠ABO=60°,又∵∠CBA=60°,∴∠CBD=60°,∠BCD=30°,∴BD=3,CD=![]() ,所以点C的坐标为(
,所以点C的坐标为(![]() ,9);
,9);
②设点A向右滑动的距离为x,根据题意得点B向上滑动的距离也为x,如图2:
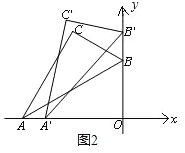
AO=12×cos∠BAO=12×cos30°=![]() ,∴A'O=
,∴A'O= ![]() ,B'O=6+x,A'B'=AB=12,在△A'O B'中,由勾股定理得,
,B'O=6+x,A'B'=AB=12,在△A'O B'中,由勾股定理得, ![]() ,解得:x=
,解得:x=![]() ,∴滑动的距离为
,∴滑动的距离为![]() ;
;
(2)设点C的坐标为(x,y),过C作CE⊥x轴,CD⊥y轴,垂足分别为E,D,如图3: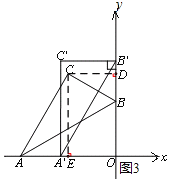
则OE=﹣x,OD=y,∵∠ACE+∠BCE=90°,∠DCB+∠BCE=90°,∴∠ACE=∠DCB,又∵∠AEC=∠BDC=90°,∴△ACE∽△BCD,∴![]() ,即
,即![]() ,∴
,∴![]() ,
, ![]() =
=![]() =
=![]() ,∴当
,∴当![]() 取最大值时,即C到y轴距离最大时,
取最大值时,即C到y轴距离最大时, ![]() 有最大值,即OC取最大值,如图,即当C'B'旋转到与y轴垂直时,此时OC=12,故答案为:12.
有最大值,即OC取最大值,如图,即当C'B'旋转到与y轴垂直时,此时OC=12,故答案为:12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程:①x﹣1=1;②x+y=2z;③2x﹣1<y;④3y﹣2=y2;⑤2x﹣y=0;⑥x﹣10>﹣5中一元一次方程的是( ),二元一次方程的是( ),一元一次不等式的是( )
A.①;⑤;⑥
B.④;⑤;⑥
C.④;②;③
D.①;②;③ -
科目: 来源: 题型:
查看答案和解析>>【题目】合并同类项:(1)(7y-3x)-(8y-5x);(2)(12a-7b)-[17a-(3b+5c)]-5c.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A(1,1),点C(a,b),满足
 +|b﹣3|=0.
+|b﹣3|=0.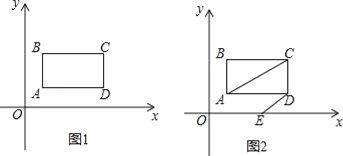
(1)求长方形ABCD的面积.
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=4时,直接写出三角形OAC的面积为 ;
②若AC∥ED,求t的值;
(3)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
①若点A1的坐标为(3,1),则点A3的坐标为 ,点A2014的坐标为 ;
②若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名
单价(元)
数量(个)
金额(元)
签字笔
3
2
6
自动铅笔
1.5
●
●
记号笔
4
●
●
软皮笔记本
●
2
9
圆规
3.5
1
●
合计
8
28
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣2a+1= .
-
科目: 来源: 题型:
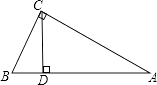
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,AB=4cm,则∠BCD= , BD= .
相关试题

