【题目】如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长. 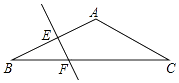
参考答案:
【答案】解:连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF为AB的垂直平分线,
∴AF=BF,
∴∠BAF=∠B=30°,
∴∠FAC=90°,
∵BF=5cm,
∴AF=5cm,
∴FC=10cm.
【解析】根据等边对等角可得∠B=∠C=30°,再根据线段垂直平分线的性质可得∠BAF=∠B=30°,进而可得∠FAC=90°,再根据在直角三角形中,30°角所对的直角边等于斜边的一半可得答案.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是它外角和的2倍,则它的边数是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒搭的图形如图所示:
(1)第一个图①有5根火柴棒,第二个图②有9根火柴棒,第三个图③有 根火柴棒;
(2)按此规律,第n个图有 根火柴棒;(用含n的式子表示)
(3)按此规律,是否存在第n个图有2018根火柴棒?若存在,请求出n的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线
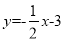 与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).(1)求抛物线的解析式;
(2)点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大,若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;
(3)过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列命题中,正确的是( )
A.两组对边分别平行的四边形是矩形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.一组邻边相等的矩形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式2a+b表示的实际意义: .
相关试题

