搜索
【题目】设m、n是一元二次方程x2+2x﹣7=0的两个根，则m2+3m+n=
参考答案：
【答案】5
【解析】解：∵设m、n是一元二次方程x2+2x﹣7=0的两个根， ∴m+n=﹣2，
∵m是原方程的根，
∴m2+2m﹣7=0，即m2+2m=7，
∴m2+3m+n=m2+2m+m+n=7﹣2=5，
所以答案是：5．
【考点精析】解答此题的关键在于理解根与系数的关系的相关知识，掌握一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC为等边三角形，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则三个结论正确的是
①P在∠A的平分线上；②QP∥AR；③△BRP≌△QSP．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果代数式2amb4与﹣5a2bn+1是同类项，则m＝_____，n＝_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个多边形的内角和是它外角和的2倍，则它的边数是___．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用火柴棒搭的图形如图所示：
（1）第一个图①有5根火柴棒，第二个图②有9根火柴棒，第三个图③有 根火柴棒；
（2）按此规律，第n个图有 根火柴棒；（用含n的式子表示）
（3）按此规律，是否存在第n个图有2018根火柴棒？若存在，请求出n的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=AC，∠BAC=120°，EF为AB的垂直平分线，EF交BC于F，交AB于E，BF=5cm，求CF的长．
-
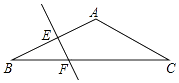
科目： 来源： 题型：
查看答案和解析>>【题目】已知:如图,直线
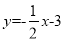与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2，0).(1)求抛物线的解析式;
(2)点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大,若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;
(3)过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.
相关试题
