【题目】某楼盘一楼是车库(暂不出售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为4000元![]() 米
米![]() ,从第八层起每上升一层.每平方米的售价增加50元;反之,楼层每下降一层,每平方米的售价减少30元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:方案一:购买者先交纳首付金额(商品房总价的
,从第八层起每上升一层.每平方米的售价增加50元;反之,楼层每下降一层,每平方米的售价减少30元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:方案一:购买者先交纳首付金额(商品房总价的![]() ,再办理分期付款(即贷款).方案二:购买者若一次付清所有房款,则享受
,再办理分期付款(即贷款).方案二:购买者若一次付清所有房款,则享受![]() 的优惠,并免收五年物业管理费(已知每月物业管理费为
的优惠,并免收五年物业管理费(已知每月物业管理费为![]() 元).
元).
(1)请用含楼层(![]() ,
,![]() 是正整数)的代数式表示售价y(元/平方米);
是正整数)的代数式表示售价y(元/平方米);
(2)小张已筹到160000元,若用方案一购房,他可以首付哪些楼层的商品房呢?
(3)老王想在此楼盘买房,有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接再多享受![]() 的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
参考答案:
【答案】(1)![]() ;(2)任意购买2层到16楼层的商品房;(3)不一定正确,理由见解析
;(2)任意购买2层到16楼层的商品房;(3)不一定正确,理由见解析
【解析】
(1)分类讨论:2≤x≤8,8<x≤23,根据楼层的价格变化,可得函数解析式;
(2)分类讨论:2≤x≤8,8<x≤23,根据首付款与筹备款的不等式关系,可得答案;
(3) 根据方案二的方法,可得房款的关系式,再根据不免物业费直接享受9%的优惠,可得函数关系式,再根据不等式的关系,可得答案.
(1)每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式为y=![]() ;
;
(2)由(2)得当2≤x≤8时,(30x+3760)×120×30%=36(30x+3760),
当x=8时,36(30×8+3760)=144000<160000,
所以可以到2楼到8楼的楼层可任意选;
当8<x≤23时,(50x+3600)×120×30%=36(50x+3600)≤160000,
x<![]() ,x是正整数且8<x≤16,9层到16层任意楼层都可以购买,
,x是正整数且8<x≤16,9层到16层任意楼层都可以购买,
综上所述,用方案一购房,他可以任意购买2层到16楼层的商品房;
(3)方案二y1=(50×16+3600)×120×(1-8%),
老王的想法y2=(50×16+3600)×120×(1-9%)+12×5a,
y1-y2=5280-60a,
当y1>y2时,即y1-y2=5280-60a>0,
0<a<88,想法正确,
当y1<y2时,y1-y2=5280-60a<0,
a>88,想法不正确,
因此,老王的说法不一定正确.
-
科目: 来源: 题型:
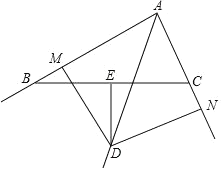
查看答案和解析>>【题目】如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出
 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价) -
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2分)矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长是()
A. 16 B. 22或16 C. 26 D. 22或26
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形的一个内角平分线把矩形的一条边分成3cm和5cm两部分,则矩形的周长( )
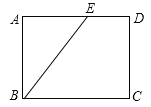
A. 16cm B. 22cm和16cm C. 26cm D. 22cm和26cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是( )
A. 57.5° B. 32.5° C. 57.5°,23.5° D. 57.5°,32.5°
相关试题

