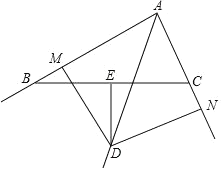
【题目】如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.
参考答案:
【答案】(1)见解析;(2)2
【解析】
(1)根据角平分线的性质和线段垂直平分线的性质可得到DM=DN,DB=DC,根据HL证明Rt△DMB≌Rt△DNC,即可得出BM=CN;
(2)由HL证明Rt△DMA≌Rt△DNA,得出AM=AN,证出2BM=AB-AC=4,即可得出BM=2.
(1)证明:连接BD、CD,如图所示:
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
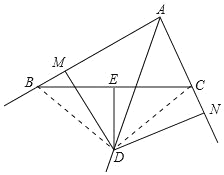
∵DE垂直平分线BC,
∴DB=DC,
在Rt△DMB和Rt△DNC中,
![]()
∴Rt△DMB≌Rt△DNC(HL),
∴BM=CN;
(2) 由(1)得:BM=CN,
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△DMA和Rt△DNA中,
![]()
∴Rt△DMA≌Rt△DNA(HL),
∴AM=AN,
∵AM=AB-BM,AN=AC+CN,
∴AB-BM=AC+CN,
∴2BM=AB-AC=8-4=4,
∴BM=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对
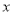 ,
,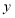 定义一种新运算
定义一种新运算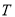 ,规定:
,规定: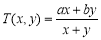 (其中
(其中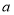 ,
,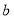 均为非零常数),这里等式右边是通常的四则运算,例如:
均为非零常数),这里等式右边是通常的四则运算,例如: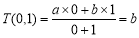 ,已知
,已知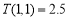 ,
, .
.(1)求
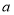 ,
,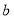 的值;
的值;(2)若关于
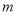 的不等式组
的不等式组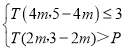 恰好有2个整数解,求实数
恰好有2个整数解,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有四张背面相同的纸牌A,B,C,D,其正面分别划有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.
(1)用树状图(或列表法)表示两次模牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张牌面图形既是中心对称图形又是轴对称图形的纸牌的概率.
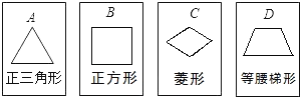
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
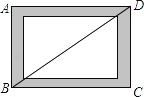
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出
 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价) -
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某楼盘一楼是车库(暂不出售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为4000元
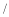 米
米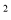 ,从第八层起每上升一层.每平方米的售价增加50元;反之,楼层每下降一层,每平方米的售价减少30元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:方案一:购买者先交纳首付金额(商品房总价的
,从第八层起每上升一层.每平方米的售价增加50元;反之,楼层每下降一层,每平方米的售价减少30元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:方案一:购买者先交纳首付金额(商品房总价的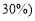 ,再办理分期付款(即贷款).方案二:购买者若一次付清所有房款,则享受
,再办理分期付款(即贷款).方案二:购买者若一次付清所有房款,则享受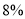 的优惠,并免收五年物业管理费(已知每月物业管理费为
的优惠,并免收五年物业管理费(已知每月物业管理费为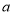 元).
元).(1)请用含楼层(
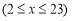 ,
,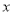 是正整数)的代数式表示售价y(元/平方米);
是正整数)的代数式表示售价y(元/平方米);(2)小张已筹到160000元,若用方案一购房,他可以首付哪些楼层的商品房呢?
(3)老王想在此楼盘买房,有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接再多享受
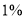 的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
相关试题

