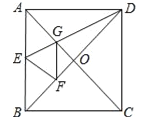
【题目】如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是![]() ,其中正确的结论个数为( )
,其中正确的结论个数为( )
A.2 B.3 C.4 D.5
参考答案:
【答案】B.
【解析】
试题分析:∵四边形ABCD是正方形,∴∠GAD=∠ADO=45°,由折叠的性质可得:∠ADG=![]() ∠ADO=22.5°,故①正确.
∠ADO=22.5°,故①正确.
∵由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,∴AE=EF<BE,∴AE<![]() AB,∴
AB,∴![]() >2,故②错误.
>2,故②错误.
∵∠AOB=90°,∴AG=FG>OG,△AGD与△OGD同高,∴S△AGD>S△OGD,故③错误.
∵∠EFD=∠AOF=90°,∴EF∥AC,∴∠FEG=∠AGE,∵∠AGE=∠FGE,∴∠FEG=∠FGE,∴EF=GF,∵AE=EF,∴AE=GF,故④正确.
∵AE=EF=GF,AG=GF,∴AE=EF=GF=AG,∴四边形AEFG是菱形,∴∠OGF=∠OAB=45°,∴EF=GF=![]() OG,∴BE=
OG,∴BE=![]() EF=
EF=![]() ×
×![]() OG=2OG.
OG=2OG.
故⑤正确.
∵四边形AEFG是菱形,∴AB∥GF,AB=GF.
∵∠BAO=45°,∠GOF=90°,∴△OGF时等腰直角三角形.
∵S△OGF=1,∴![]() =1,解得OG=
=1,解得OG=![]() ,∴BE=2OG=
,∴BE=2OG=![]() ,GF=
,GF=![]() =
=![]() =2,∴AE=GF=2,∴AB=BE+AE=
=2,∴AE=GF=2,∴AB=BE+AE=![]() ,∴S正方形ABCD=
,∴S正方形ABCD=![]() =
=![]() =
=![]() ,故⑥错误,∴其中正确结论的序号是:①④⑤.
,故⑥错误,∴其中正确结论的序号是:①④⑤.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x-3)(x2-4x+1)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y-3)(y+1)+4 (第一步)
= y2-2y+1 (第二步)
=(y-1)2 (第三步)
=(x2-4x-1)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑车从邮局O出发,先向西骑行2km到达A村,继续向西骑行3km到达B村,然后向东骑行8km,到达C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1cm表示2km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村距离A村有多远?
(3)邮递员共骑行了多少km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知13 = 1 =
 ×12×22, 13+23=9=
×12×22, 13+23=9= ×22×32,13 + 23 + 33 = 36 =
×22×32,13 + 23 + 33 = 36 = ×32×42, …,按照这个规律完成下列问题:
×32×42, …,按照这个规律完成下列问题:(1)13+23+33+43+53=________=
 × ( )2 × ( )2
× ( )2 × ( )2(2)猜想:13+23+33+…+n3=___________
(3)利用(2)中的结论计算:(写出计算过程)
113+123 + 313+143 + 153+163 + ……+393+403.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣π2x2y的系数是_____,次数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:
 观察由※组成的图案和算式,解答问题:
观察由※组成的图案和算式,解答问题:1+3=4=

1+3+5=9=

1+3+5+7=16=

1+3+5+7+9=25=

(1)请猜想1+3+5+7+9+ … +29= ;(3分)
(2)请猜想1+3+5+7+9+ … +(2n-1)+(2n+1)= ;(3分)
(3)请用上述规律计算:(6分)41+43+45+ …… +77+79
相关试题

